CRF 算法

1. CRF 算法基本原理

一般地，在 NLP 中是

  • 输入单词序列经过 BiLSTM 或BERT处理，生成每个单词的特征表示
  • 然后将特征表示输入到 CRF 层，如下图所示，就是 BiLSTM+CRF 的框架图。

不直接接一个 softmax 层是因为，上一个标签是对后续标签有约束的，CRF 就是学习这个约束的过程，最后使得输出更合理。

CRF 算法

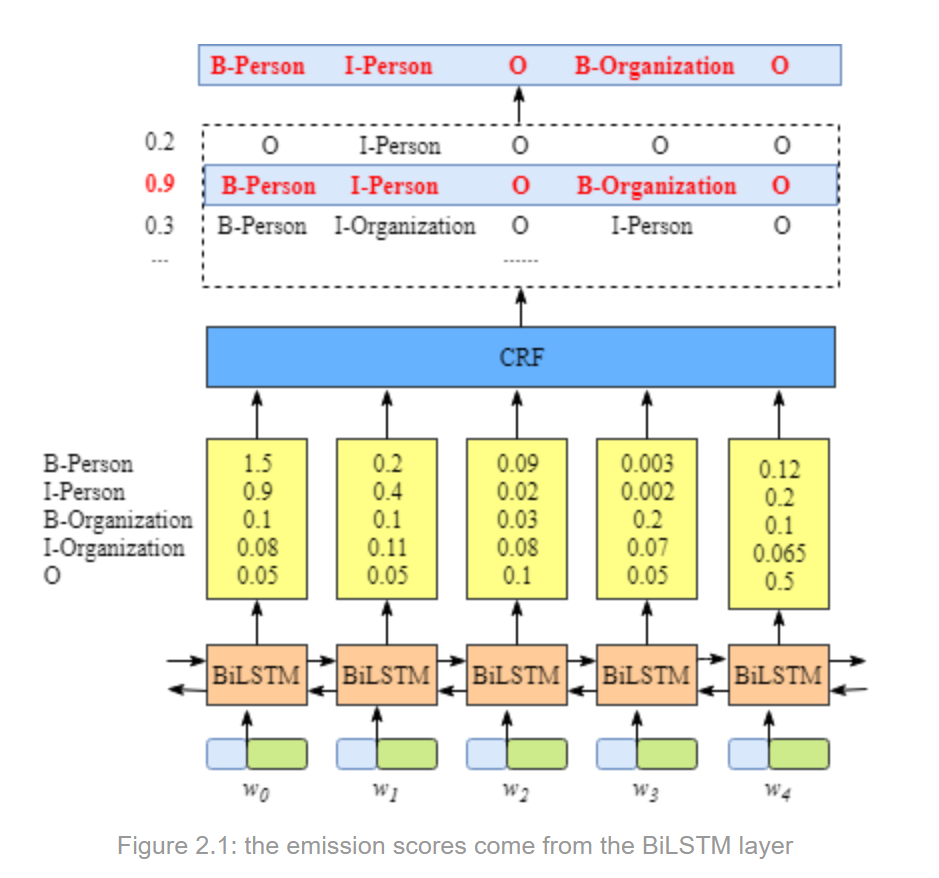
因为前的特征表示过程是很简单的，对应 BERT 类你只要类似文本分类一样输入，取 bert 输出的 Output[0]，即 (bs, seq_len, hidden_dim) 输出矩阵，“喂”到 CRF 层即可。

CRF 算法

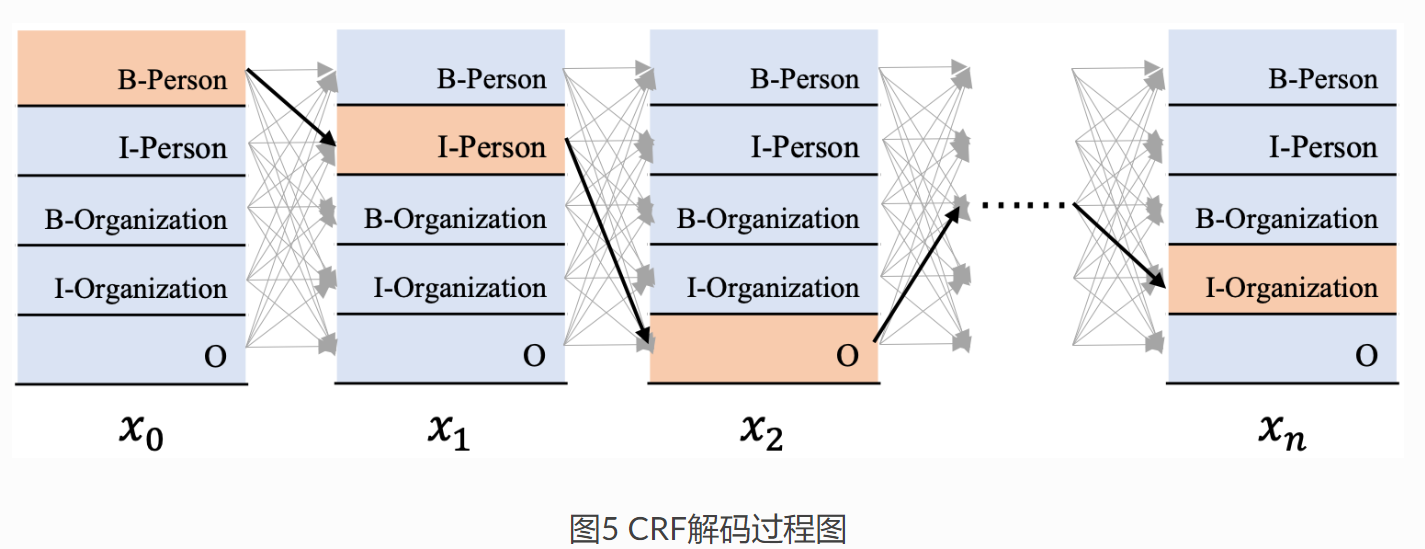
如图所示 CRF 接码过程图中所示。

假定输入为 $x=[x_0, x_1, x_2, x_n]$ (这里的 x 表示输入文本对应的发射分数，每个词 $x_i$ 都对应一个发射向量，维度为标签数目)。

输出为 $y=[y_0, y_1, \cdots, y_n]$ 那么其条件概率表示为：
$$
P(y|x) = P(y_0, y_1, \cdots, y_n|x_0, x_1, \cdots, x_n) \tag{1}
$$
例如，我们输入文本对应的标签序列：B-Person, I-Person, O, O，B-Org I-Org。那么这个序列的转移分数可按照如下方式计算：
$$
\text{Seq}_t = T_{I-\text{Person},B-\text{Person}} + T_{O,I-\text{Person}} + T_{O,O} + T_{O,B-\text{Org}} + T_{B-\text{Org}, I-\text{Org}}
$$
而 CRF 解码策略要求输出路径在所有的路径中概率最大。假设标签数量为 $k$, 输入文本长度为 $n$, 显然会有 $N=k^n$ 条路径，第 $i$ 条路径分数记为 $S_i$. 那么输出序列 $i$ 的概率为：
$$
P(S_i) = \frac{e^{S_i}}{\sum_j^{N}e^{S_j}} \tag{2}
$$
表示输出序列 $i$ 比所有路径的分数。

我们的模板就是使得真实路径 $P(S_{Real})$ 最大，为了方便计算，我们加上负号最小化这个 loss：
$$
\text{loss} = -P(S_{Real}) =-\frac{e^{S_{\text{Real}}}}{\sum_j^{N}e^{S_j}} \tag{3}
$$
式 3 取对数有：
$$
\begin{aligned}
\text{loss} &= -\log \frac{e^{S_{real}}}{\sum_j^{N}{e^{S_j}}} \\
&= -(\log(e^{S_{real}}) – \log(\sum_j^{N}{e^{S_j}})) \\
&= \log(\sum_j^{N}{e^{S_j}}) – \log(e^{S_{real}}) \\
&= \log(e^{S_1}+e^{S_2}+…+e^{S_N}) – S_{real} \\
\end{aligned} \tag{4}
$$
这就是 CRF 建模的损失函数，即等于 所有路径分数 exp 和的 log 减去 单条真实路径分数$ S_{real}$。这样我们只要计算每条路径的分数了，为了方便计算先约定一些记号。

2.CRF 参数和路径分数计算公式

Tag Tag id
B-Person 0
I-Person 1
B-Org 2
I-Org 3
O 4

为了方便将 Tag 映射为 Tag id, 一般在代码中会有 label2id = {label: i for i, label in enumerate(labels)} 来维护一个字典，方便后续查找。

  1. 发射分数矩阵为 $E$, shape 为 $[n, \text{tag_size}]$。每行表示输入文本的一个 token 的发射分数。
  2. 转移分数矩阵为 $T$, shape 为 $[\text{tag_size}, \text{tag_size}]$, 表示每个 Tag 转移到下一个 Tag 的分数。比如 $T_{03}$ 表示 B -Person 转移到 I -Org 的分数，那么这个 T 矩阵上该位置的数值就是对应分数。

我们知道，每条路径分数就是从发射分数到转移分数的路径组合计算得来的。如上图 5 中黄色路径中，

  • $x_0$ 的标签是 B -Person, 发射分数为 $E_{00}$
  • 接下来 $x_1$ 的标签是 $I-Person$，对应发射分数为 $E_{11}$
  • 而由 B -person 像 I -Person 转移的分数是 $T_{10}$。到这里的分数就是 $E_{00}+T_{10}+E_{11}$
  • 接下来是 $x_2$, 标签是 O。这里 $x_1$ 的标签 $I-Person$ 像 $x_2$ 标签 O 转移的分数为 $T_{41}$。到这步的分数是 $E_{00}+T_{10}+E_{11}+T_{41}+E{24}$.

推导整条路径分数计算公式为：
$$
S_{real}=\sum_{i=0}^{n-1}{E_{i,y_i}} + \sum_{i=0}^{n-2}{T_{y_{i+1}, y_{i}}} \tag{5}
$$

3. 前向算法

要优化 CRF 路径，就是优化 loss。根据公式 4，要计算所有路径分数和真实路径分数。实际上所有路径分数计算需要进行 log sum exp 计算，本身很复杂。另外假设有长度为 50 的文本，标签数量为 31，那么整个路径数目为 $31^{50}$，计算代价太高了，训练和预测速度将非常慢。

实际上，使用称为 前向算法 的动态规划。它会将所有路径和计算，拆解为每个位置和计算，最终得出所有路径和。3

由式 4 可知所有路径和分数是：
$$
\log(e^{S_1}+e^{S_2}+…+e^{S_N}) \tag{6}
$$

下面来介绍其计算原理，为了简化计算量，只使用 2 个 tag，3 个词。如下图所示。

假定其发射分数矩阵 emission 为：
$$
\text{emission}i = [x{i0}, x_{i1}] \tag{7}
$$

其中, $x_i$ 表示位置为 $i$ 的词对应的发射分数，$x_{i0}$ 表示 $i$ 位置 $\text{tag}0$ 的标签的分数，$x{i1}$ 表示 $i$ 位置 $\text{tag}_1$ 的标签的分数。

转移矩阵 trans 矩阵为：
$$
\text{trans} =\left[\begin{matrix} t_{00} & t_{01}\ t_{10} & t_{11} \end{matrix} \right] \tag{8}
$$
其中, $t_{01}$ 表示从 $\text{tag}1$ 到 $\text{tag}_0$ 的转移分数，$t{10}$ 表示从 $\text{tag}_0$ 到 $\text{tag}_1$ 的转移分数。

路径分数和:
$$
\text{alpha}_i = [s_{i0}, s_{i1}] \tag{9}
$$
其中 $s_{i0}$ 表示从到 $i$ 位置为止，以标签 $\text{tag}0$ 结尾的所有路径分数。具体来说，$\text{alpha}_2 = [s_{20}, s_{21}]$ 表示到 $x_2$ 位置，这里理论上会是所有 tag，但这里简化了只设定 2 个 tag，那么就是以 $\text{tag}0$ 结尾的所有路径和 + 以 $\text{tag}_1$ 结尾的所有路径分数。比如下图中 $s{20}$ 就表示了：
$$
x_{00},x_{10},x_{20}\\
x_{00},x_{11},x_{20}\\
x_{01},x_{10},x_{20}\\
x_{01},x_{11},x_{20}
$$
这四条路径的分数。

CRF 算法

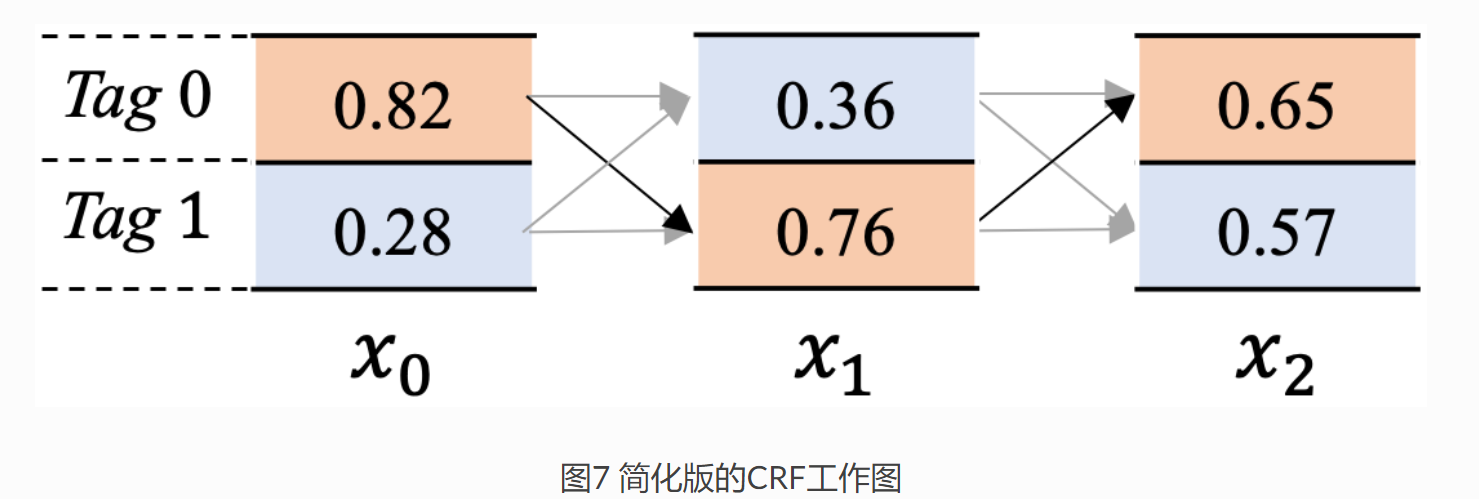
下面来具体看看路径分数的计算，如果计算到 $x_2$, 需要 3 个步骤，这里只介绍到 $x_1$，后续计算类似推导。

  1. 截止到 $x_0$ 位置。

该位置发射分数为 $\text{emission}_0 = [x_{00}, x_{01}]$, 这里是序列起始位置，该位置路径分数和为 $\text{alpha}_0 = [s_{00}, s_{01}]=[x_{00}, x_{01}]$。路径分数计算为：
$$
\text{total}_0 = \log (e^{x{00}} + e^{x_{01}}) \tag{10}
$$

  1. 截止到 $x_1$ 位置

这步就有 $x_0$ 向 $x_1$ 位置转移的过程，会复杂一些。$x_1$ 位置的发射分数为：
$$
\text{emission}_1 = [x_{10}, x_{11}]
$$
转移概率矩阵为:
$$\text{trans} =\left[\begin{matrix} t_{00} & t_{01}\\ t_{10} & t_{11} \end{matrix} \right]$$

前一个位置路径分数 $\text{alpha}_0 =[x_{00}, x_{01}]$。

展开 $\text{emission}_1, \ \text{alpha}_0$ 两者方便后续用矩阵计算。

$$\begin{aligned}\text{emission}1 &= \left[\begin{matrix} x_{10} & x_{10}\\ x_{11} & x_{11} \end{matrix} \right] \end{aligned}$$

$$\begin{aligned}
\text{alpha}_0 &= \left[\begin{matrix} x_{00} & x_{01}\\ x_{00} & x_{01} \end{matrix} \right] \end{aligned} \tag{11}$$
那么截止到 $x_1$ 位置路径分数和计算可以表示为, 前一步 $\text{alpha}_0$+ 转移状态分数 $\text{trans}$+ 发射分数 $\text{emission}_1$. 公式计算为：

$$\begin{aligned}
\text{scores} &= \text{alpha}_0+\text{trans}+\text{emission}_1 \\ &= \left[\begin{matrix} x_{00} & x_{01}\\ x_{00} & x_{01} \end{matrix} \right] + \left[\begin{matrix} t_{00} & t_{01}\\ t_{10} & t_{11} \end{matrix} \right] + \left[\begin{matrix} x_{10} & x_{10}\\ x_{11} & x_{11} \end{matrix} \right] \\ &= \left[\begin{matrix} x_{00}+t_{00}+x_{10} & x_{01}+t_{01}+x_{10}\\ x_{00}+t_{10}+x_{11} & x_{01}+t_{11}+x_{11} \end{matrix} \right]
\end{aligned} \tag{12}$$
以第一行为例，第一行表示当前位置 $x_1$ 以 $\text{tag}_0$ 结尾的所有路径分数，那么在第一行所表示的路径分数最大的那条，就是当前位置 $x_1$ 以 $\text{tag}_0$ 结尾的分数最大路径。

那么，我们可以计算当前位置 $x_1$ 的各个标签结尾的路径分数 $\text{alpha}_1$: $$ \text{alpha}_1 = [\log(e^{x{00}+t_{00}+x_{10}}+e^{x_{01}+t_{01}+x_{10}}), \log(e^{x_{00}+t_{10}+x_{11}}+e^{x_{01}+t_{11}+x_{11}})] \tag{13}
$$
这样计算截止到 $x_1$ 位置，所有路径和为：
$$
\begin{aligned}
\text{total}_1 &= \log(e^{\text{alpha}_1[0]} + e^{\text{alpha}_1[1]}) \\ &=\log(e^{\log(e^{x_{00}+t_{00}+x_{10}}+e^{x_{01}+t_{01}+x_{10}})}+e^{\log(e^{x_{00}+t_{10}+x_{11}}+e^{x_{01}+t_{11}+x_{11}})}) \\ &=\log(e^{x_{00}+t_{00}+x_{10}}+e^{x_{01}+t_{01}+x_{10}} + e^{x_{00}+t_{10}+x_{11}}+e^{x_{01}+t_{11}+x_{11}})
\end{aligned} \tag{14}
$$
这就是到 $x_1$ 位置的所有路径和分数，也就是归一化分数。

还可以继续计算 $x_2$ 位置，但都类似，就是前一路径分数 + 转移状态分数 + 发射分数。

4. Viterbi 算法

Viterbi 算法解决的是，如何使用 CRF 从全部的路径中解码出得分最高的那条路径？

具体来说，如图 7 所示，接码得到分数最大的路径，如橙黄色所示路径。

大部分约定记号跟小节 3 一样，区别有以下：

  • $\text{alpha}_i = [s_{i0}, s_{i1}]$ 表示到 $x_i$ 位置，以 tag0 和 tag1 记为的路径中，取得的最大分数的路径。具体到图中就是 $x_{00}, x_{11}, x_{20}$ 的路径分数。
  • 另外，引入 $\text{beta}_{i} = [p_{i0}, p_{i1}]$。表示当前 $x_i$ 位置，以当前位置 $x_i$ 相应标签结尾的路径中，分数最大的路径在前一个位置即 $x_{i-1}$ 的标签索引。

如 $x_2$ 位置，$\text{beta}_{2} = [p_{20}, p_{21}]$，$p_{20}$ 表示截止到 $x_2$ 位置，以标签 tag0 结尾的最大分数路径的前一个位置的 $x_{i-1}$ 的标签索引，那么就是 $p_{20}=1$。同理,$p_{21}=1$。

  1. 截止到 $x_0$ 位置

该位置发射分数为 $\text{emission}_0 = [x_{00}, x_{01}]$, 这里是序列起始位置，该位置路径分数和为 $\text{alpha}0 =[x_{00}, x_{01}]$。$x_0$ 前面没有路径了，初始化参数 $\text{beta}_0=[-1, -1]$

  1. 截止到 $x_1$ 位置

其分数为，还是和式 12 一样。
$$\begin{aligned}
\text{scores} &= \text{alpha}0+\text{trans}+\text{emission}_1 \\ &= \left[\begin{matrix} x{00} & x_{01}\\ x_{00} & x_{01} \end{matrix} \right] + \left[\begin{matrix} t_{00} & t_{01}\ t_{10} & t_{11} \end{matrix} \right] + \left[\begin{matrix} x_{10} & x_{10}\\ x_{11} & x_{11} \end{matrix} \right] \\ &= \left[\begin{matrix} x_{00}+t_{00}+x_{10} & x_{01}+t_{01}+x_{10}\\ x_{00}+t_{10}+x_{11} & x_{01}+t_{11}+x_{11} \end{matrix} \right]
\end{aligned}
$$
同样地，第一行表示当前位置 $x_1$ 以 tag0 结尾的所有路径的得分，真是路径是取两个分数中国最大的。因此，我们可以算出到 $x_1$ 各个标签的最大路径分数 $\text{alpha}_1$。具体公式为：$$ \begin{aligned} \text{alpha}_1 &= [\max(\text{scores}[0,0],\ \text{scores}[0,1]),\ \max(\text{scores}[1,0],\ \ \text{scores}[1,1])] \\ &= [\max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}), \max(x_{00}+t_{10}+x_{11},\ x_{01}+t_{11}+x_{11})]
\end{aligned} \tag{15}
$$
这里就是，若以 tag0 标签结尾，那么路径有 $x_{00}+t_{00}+x_{10}$ 和 $x_{01}+t_{01}+x_{10}$, 其中较大这就是我们需要的最大路径。

不妨假设：
$$
x_{00}+t_{00}+x_{10} < x_{01}+t_{01}+x_{10}\\ x_{00}+t_{10}+x_{11} > x_{01}+t_{11}+x_{11}
$$
这样可以看出 $x_1$ 的索引位置为 $\text{beta}_{1} = [1, 0]$。因为 $x{00}+t_{00}+x_{10} < x_{01}+t_{01}+x_{10}$ 表示 tag0 结尾的路径中较大的是 $x_01$，即前一步是 tag1。

  1. 截止到 $x_2$ 位置。

发射分数 $\text{emission}_2 = [x_{20}, x_{21}]$, 转移概率矩阵为：
$$
\text{trans} =\left[\begin{matrix} t_{00} & t_{01}\ t_{10} & t_{11} \end{matrix} \right]
$$
$x_2$ 前一个位置各个标签路径累积和:
$$
\text{alpha}_1=[\max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}),\ \max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11})]
$$
展开发射矩阵和路径分数和：
$$
\text{alpha}_2 = \left[\begin{matrix} \max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}) & \max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11}) \\ \max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}) & \max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11}) \end{matrix} \right]
$$
那么 $x_2$ 位置的每条分数为：
$$
\begin{aligned}
\text{scores} &= \text{alpha}1+\text{trans}+\text{emission}_2 \\ &= \left[\begin{matrix} \max(x{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}) & \max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11}) \\ \max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}) & \max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11}) \end{matrix} \right] + \left[\begin{matrix} t_{00} & t_{01}\ t_{10} & t_{11} \end{matrix} \right] + \left[\begin{matrix} x_{20} & x_{20}\ x_{21} & x_{21} \end{matrix} \right] \\ &= \left[\begin{matrix} \max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}) +t_{00}+x_{20} & \max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11})+t_{01}+x_{20}\\ \max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10})+t_{10}+x_{21} & \max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11}) +t_{11}+x_{21} \end{matrix} \right]
\end{aligned} \tag{16}
$$
这样就可以算出当前 $x_2$ 位置的最大路径分数 $\text{alpha}_2$: $$ \begin{aligned} \text{alpha}_2 &= [\max(scores[0,0], scores[0,1]), \max(scores[1,0], scores[1,1])] \\ &= [\max( \max(x{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}) +t_{00}+x_{20}, \max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11})+t_{01}+x_{20}), \\
&\qquad \max(\max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10})+t_{10}+x_{21}, \max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11}) +t_{11}+x_{21}
)]
\end{aligned} \tag{17}
$$
不妨假设：
$$\begin{aligned}
\max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}) +t_{00}+x_{20} > \max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11})+t_{01}+x_{20}) \\
\max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}) +t_{10}+x_{21} < \max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11})+t_{11}+x_{21}) \end{aligned}\tag{18}$$
其实式 18 很容易理解，只是看起来复杂，只是表示前一步 tag 转换到下一步分数比较。

上一步中假设：
$$\begin{aligned}
x_{00}+t_{00}+x_{10} < x_{01}+t_{01}+x_{10}\ x_{00}+t_{10}+x_{11} > x_{01}+t_{11}+x_{11}\end{aligned}\tag{19}
$$
代入式 18 有：
$$
x_{01}+t_{01}+x_{10}+t_{01}+x_{10} < x_{00}+t_{10}+x_{11}+t_{01}+x_{20}\\ x_{01}+t_{01}+x_{10}+t_{10}+x_{21} > x_{00}+t_{10}+x_{11}+t_{11}+x_{21} \tag{20}
$$
因此 $x_2$ 位置的索引 $\text{beta}_2 = [1, 0]$, 因为 $x_{00}+t_{10}+x_{11}+t_{01}+x_{20}$ 表示 tag0 是前一步 tag1 经过 $t_{01}$ 转换为 $x_{20}$。同理可得 tag1 是 tag0 而来，当然这个比较就是路径分数最大化的过程。

此时，
$$
\text{alpha}2 = [x_{00}+t_{10}+x_{11}+t_{01}+x_{20}, x_{01}+t_{01}+x_{10}+t_{10}+x_{21} ] \tag{21}
$$
图 7 中橙黄色路径分数高，因此有：
$$
x_{00}+t_{10}+x_{11}+t_{01}+x_{20} > x_{01}+t_{01}+x_{10}+t_{10}+x_{21} \tag{22}
$$
这表示 $x_2$ 位置所有标签对应的最大路径中以 tag0 结尾的是最大的。

  1. 开始解码标签序列
  2. 因为我们有 $\text{beta}_{i} = [p_{i0}, p_{i1}]$ 这个前一步最大标签的索引，那么如果 $x_2$ 位置 tag0 最大，$\text{beta}_2 = [1, 0]$，其前一步 $x_1$ 应该取 1，表示 tag1.
  3. 到 $x_1$ 位置，这时取 tag1, 前一步 $x_0$ 中 $\text{beta}_{1} = [1, 0]$，那么应该取 $0$, 即 tag0
  4. 最后到 $\text{beta}_0=[-1, -1]$, 就结束了，因此输出的最大路径就是 tag0->tag1->tag0.

5.pytoch-crf 中实现

一般使用 pytorch-crf 包中的 CRF 类，其继承自 nn.Module。class CRF(nn.Module): 中最重要的就是:

def forward(
            self,
            emissions: torch.Tensor,
            tags: torch.LongTensor,
            mask: Optional[torch.ByteTensor] = None,
            reduction: str = 'sum',
    ) -> torch.Tensor:

def decode(self, emissions: torch.Tensor,
               mask: Optional[torch.ByteTensor] = None) -> List[List[int]]:
    self._validate(emissions, mask=mask)
        if mask is None:
            mask = emissions.new_ones(emissions.shape[:2], dtype=torch.uint8)

        if self.batch_first:
            emissions = emissions.transpose(0, 1)
            mask = mask.transpose(0, 1)

        return self._viterbi_decode(emissions, mask)

一般实例化一个 crf:

from torchcrf import CRF
crf = CRF(num_labels, batch_first=True)
  1. forward用来计算 loss, 用于 训练。loss = - crf(seq_out, labels, mask=attention_mask.bool(), reduction='mean')
  2. decode用来输出 logits, 用于 预测解码。logits = crf.decode(seq_out, mask=attention_mask.bool()).

forward 部分：

    def forward(
            self,
            emissions: torch.Tensor,
            tags: torch.LongTensor,
            mask: Optional[torch.ByteTensor] = None,
            reduction: str = 'sum',
    ) -> torch.Tensor:
        """Compute the conditional log likelihood of a sequence of tags given emission scores.

        Args:
            emissions (`~torch.Tensor`): Emission score tensor of size
                ``(seq_length, batch_size, num_tags)`` if ``batch_first`` is ``False``,
                ``(batch_size, seq_length, num_tags)`` otherwise.
            tags (`~torch.LongTensor`): Sequence of tags tensor of size
                ``(seq_length, batch_size)`` if ``batch_first`` is ``False``,
                ``(batch_size, seq_length)`` otherwise.
            mask (`~torch.ByteTensor`): Mask tensor of size ``(seq_length, batch_size)``
                if ``batch_first`` is ``False``, ``(batch_size, seq_length)`` otherwise.
            reduction: Specifies  the reduction to apply to the output:
                ``none|sum|mean|token_mean``. ``none``: no reduction will be applied.
                ``sum``: the output will be summed over batches. ``mean``: the output will be
                averaged over batches. ``token_mean``: the output will be averaged over tokens.

        Returns:
            `~torch.Tensor`: The log likelihood. This will have size ``(batch_size,)`` if
            reduction is ``none``, ``()`` otherwise.
        """
        self._validate(emissions, tags=tags, mask=mask)
        if reduction not in ('none', 'sum', 'mean', 'token_mean'):
            raise ValueError(f'invalid reduction: {reduction}')
        if mask is None:
            mask = torch.ones_like(tags, dtype=torch.uint8)

        if self.batch_first:
            emissions = emissions.transpose(0, 1)
            tags = tags.transpose(0, 1)
            mask = mask.transpose(0, 1)

        # shape: (batch_size,)
        numerator = self._compute_score(emissions, tags, mask)
        #下面是_compute_score 计算核心部分，就是前一步的转移分数 + 发射分数
        #for i in range(1, seq_length):
            ## Transition score to next tag, only added if next timestep is valid (mask == 1)
            ## shape: (batch_size,)
            #score += self.transitions[tags[i - 1], tags[i]] * mask[i]

            ## Emission score for next tag, only added if next timestep is valid (mask == 1)
            ## shape: (batch_size,)
            #score += emissions[i, torch.arange(batch_size), tags[i]] * mask[i]
        # shape: (batch_size,)
        denominator = self._compute_normalizer(emissions, mask)
        # shape: (batch_size,)
        llh = numerator - denominator

        if reduction == 'none':
            return llh
        if reduction == 'sum':
            return llh.sum()
        if reduction == 'mean':
            return llh.mean()
        assert reduction == 'token_mean'
        return llh.sum() / mask.float().sum()

而 decode 最重要的就是 _viterbi_decode 算法部分，其用 history = [] 存储最大分数的索引，然后逆序遍历得到输出标注序列。

    def _viterbi_decode(self, emissions: torch.FloatTensor,
                        mask: torch.ByteTensor) -> List[List[int]]:
        # emissions: (seq_length, batch_size, num_tags)
        # mask: (seq_length, batch_size)
        assert emissions.dim() == 3 and mask.dim() == 2
        assert emissions.shape[:2] == mask.shape
        assert emissions.size(2) == self.num_tags
        assert mask[0].all()

        seq_length, batch_size = mask.shape

        # Start transition and first emission
        # shape: (batch_size, num_tags)
        score = self.start_transitions + emissions[0]
        history = []

        # score is a tensor of size (batch_size, num_tags) where for every batch,
        # value at column j stores the score of the best tag sequence so far that ends
        # with tag j
        # history saves where the best tags candidate transitioned from; this is used
        # when we trace back the best tag sequence

        # Viterbi algorithm recursive case: we compute the score of the best tag sequence
        # for every possible next tag
        for i in range(1, seq_length):
            # Broadcast viterbi score for every possible next tag
            # shape: (batch_size, num_tags, 1)
            broadcast_score = score.unsqueeze(2)

            # Broadcast emission score for every possible current tag
            # shape: (batch_size, 1, num_tags)
            broadcast_emission = emissions[i].unsqueeze(1)

            # Compute the score tensor of size (batch_size, num_tags, num_tags) where
            # for each sample, entry at row i and column j stores the score of the best
            # tag sequence so far that ends with transitioning from tag i to tag j and emitting
            # shape: (batch_size, num_tags, num_tags)
            next_score = broadcast_score + self.transitions + broadcast_emission

            # Find the maximum score over all possible current tag
            # shape: (batch_size, num_tags)
            next_score, indices = next_score.max(dim=1)

            # Set score to the next score if this timestep is valid (mask == 1)
            # and save the index that produces the next score
            # shape: (batch_size, num_tags)
            score = torch.where(mask[i].unsqueeze(1), next_score, score)
            history.append(indices)

        # End transition score
        # shape: (batch_size, num_tags)
        score += self.end_transitions

        # Now, compute the best path for each sample

        # shape: (batch_size,)
        seq_ends = mask.long().sum(dim=0) - 1
        best_tags_list = []

        for idx in range(batch_size):
            # Find the tag which maximizes the score at the last timestep; this is our best tag
            # for the last timestep
            _, best_last_tag = score[idx].max(dim=0)
            best_tags = [best_last_tag.item()]

            # We trace back where the best last tag comes from, append that to our best tag
            # sequence, and trace it back again, and so on
            for hist in reversed(history[:seq_ends[idx]]):
                best_last_tag = hist[idx][best_tags[-1]]
                best_tags.append(best_last_tag.item())

            # Reverse the order because we start from the last timestep
            best_tags.reverse()
            best_tags_list.append(best_tags)

        return best_tags_list

我们可以看到 Viterbi 算法就是利用动态规划不断计算当前位置的最大分数路径，同时记录前一步索引，最后来回溯整个序列。使得计算复杂度降低，计算效率增加。

Viterbi 算法的时间复杂度和空间复杂度取决于状态和观测序列的长度。假设状态序列长度为 N，观测序列长度为 T。

时间复杂度：Viterbi 算法的时间复杂度为 $O(N^2 * T)$，其中 N 是状态的数量，T 是观测序列的长度。这是因为在每个观测时间步，需要计算每个状态的最大概率，并选择最优路径。对于每个状态，需要计算其与前一个时间步所有状态的转移概率乘积，并选择最大值。因此，需要进行 N 次乘法和比较操作。

空间复杂度：Viterbi 算法的空间复杂度为 $O(N * T)$，其中 N 是状态的数量，T 是观测序列的长度。在算法执行过程中，需要维护一个 $N * T$ 的矩阵，用于存储每个状态在每个时间步的最大概率值。此外，还需要保存一个 $N * T$ 的矩阵，用于回溯最优路径。

需要注意的是，如果状态和观测的数量非常大，Viterbi 算法的复杂度可能会变得很高。在实际应用中，为了减少计算量，常常使用一些技巧和优化方法来降低复杂度，例如利用稀疏矩阵表示、剪枝策略等。

6. pytorch-crf 一般使用

import torch
from torchcrf import CRF

num_tags = 5
seq_len = 3
batch_size = 2
model = CRF(num_tags, batch_first=True)

emission = torch.randn(batch_size, seq_len, num_tags)
tags = torch.tensor([[0, 1, 2],
     [2, 4, 3],
     ], dtype=torch.long)

print(emission)
print(tags)
score = model(emission, tags)
print(score)
#引入 mask
mask = torch.tensor([[1, 1, 1], [1, 1,0]], dtype=torch.bool)
score = model(emission, tags, mask=mask)
print(score)
seq_tags =model.decode(emission, mask)
print(seq_tags)

Inference

[1] 一文读懂 BiLSTM+CRF 实现命名实体识别

[2] CRF Layer on the Top of BiLSTM

[3] 12-BiLSTM 和 CRF 算法的序列标注原理

[4] pytorch-crf

正文完
CRF
发表至： NLP
2023-11-26
 
admin
版权声明：本站原创文章，由 admin 2023-11-26发表，共计15849字。
转载说明：除特殊说明外本站文章皆由CC-4.0协议发布，转载请联系tensortimes@gmail.com。
基于gemini SQL问答
HMM算法
LLama3 model代码解析
torchchat中简单的对称量化实现
评论（没有评论）
验证码