原理
机器学习可以大致分为 无监督学习和有监督学习 两大类别(半监督学习在此不予讨论)。在无监督学习中,数据不具有预先定义的标签信息。
聚类算法是无监督学习中常用的方法之一,用于将数据样本按照相似性或距离度量分成不同的群组。其中,一些常见的聚类算法包括 K -means、层次聚类算法和 DBSCAN 等。本文主要介绍 K -means 算法。
聚类算法在许多应用场景中得到广泛应用,例如客户群体分析、社交网络分析以及数据预处理和半监督学习等间接应用。
K-means 算法的具体流程如下:
- 初始化 k 个聚类中心点(通常随机选择)。
- 计算每个样本与 k 个聚类中心的距离,并将每个样本分配到距离最近的聚类中心所属的簇中。
- 更新 k 个聚类的中心,即计算每个簇中数据点的均值作为新的聚类中心。
- 重复步骤 2 和步骤 3,直到 k 个聚类中心不再发生移动或达到预定的停止条件。
1. 分析 iris 数据
接下来我们使用 iris dataset 来探索 KMeans 作用和从零构建 KMeans。
| from sklearn import datasets | |
| import matplotlib.pyplot as plt | |
| import pandas as pd | |
| import numpy as np | |
| from sklearn.cluster import KMeans | |
| iris = datasets.load_iris() | |
| ========================== | |
| iris.feature_names | |
| ['sepal length (cm)', | |
| 'sepal width (cm)', | |
| 'petal length (cm)', | |
| 'petal width (cm)'] |
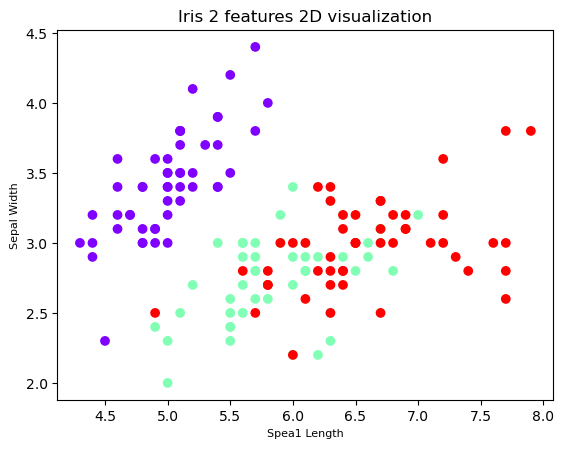
对前 2 个特征 花瓣长度和宽度 可视化如下图
| #'sepal length (cm)', | |
| # 'sepal width (cm)', | |
| #前两列数据代表花瓣长度和宽度 | |
| X = iris.data[:, :2] | |
| y = iris.target | |
| # 将数据集中所有数据进行二维可视化展示 | |
| plt.scatter(X[:,0], X[:,1], c=y, cmap='rainbow') | |
| plt.xlabel('Spea1 Length', fontsize=8) | |
| plt.ylabel('Sepal Width', fontsize=8) | |
| plt.title('Iris 2 features 2D visualization', fontsize=12) | |
| plt.show() |
PCA 降维后 3D 可视化如下:
| # 为了更好理解数据集,使用 PCA 降维,观察 3D 模式下数据的分布 | |
| import matplotlib.pyplot as plt | |
| from mpl_toolkits.mplot3d import Axes3D | |
| from sklearn.decomposition import PCA | |
| fig = plt.figure(1, figsize=(8, 8)) | |
| ax = fig.add_subplot(111, projection='3d') | |
| # ax = Axes3D(fig, elev=-150, azim=110) | |
| #将数据降到 3 维,接下来方便 3 维展示 | |
| X_reduced = PCA(n_components=3).fit_transform(iris.data) | |
| ax.scatter(X_reduced[:, 0], X_reduced[:, 1], X_reduced[:, 2], c=y, | |
| cmap='rainbow', edgecolor='k', s=40) | |
| ax.set_title("PCA Modeling") | |
| ax.set_xlabel("1st eigenvector") | |
| ax.set_ylabel("2nd eigenvector") | |
| ax.set_zlabel("3rd eigenvector") | |
| ax.view_init(elev=-150, azim=110) | |
| plt.show() |
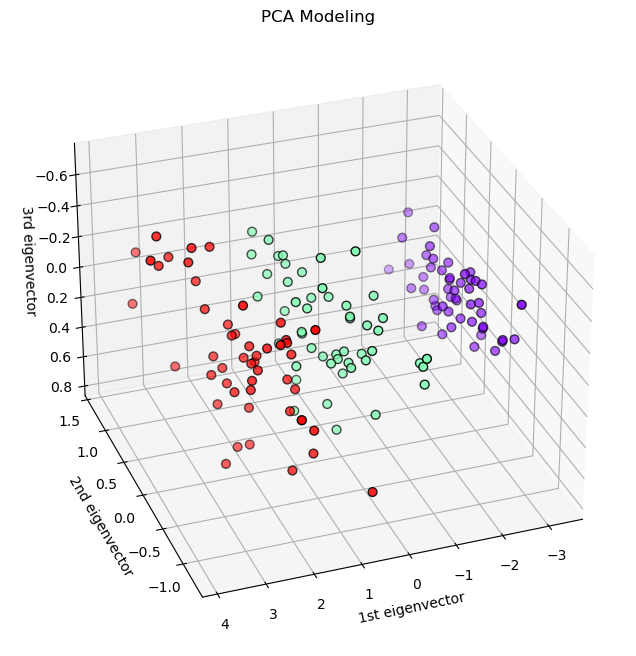
iris dataset 本身 label 就是 3 类,PCA 降维 3 维后,可以发现也差不多分为 3 簇。
2.sklearn KMeans
使用 sklearn 聚类包中的 KMeans, 得到 3 个聚类中心和
| km = KMeans(n_clusters=3, n_init='auto') | |
| km.fit(X) | |
| # 打印聚类后各个簇的中心点 | |
| centers = km.cluster_centers_ | |
| print(centers) | |
| ====================================== | |
| [[6.82391304 3.07826087] | |
| [5.8 2.7] | |
| [5.00392157 3.40980392]] |
3. 从零构建 KMeans
| class KMeans: | |
| def __init__(self, n_clusters, max_iter=100): | |
| self.n_clusters = n_clusters | |
| self.max_iter = max_iter | |
| def fit(self, X): | |
| # 随机初始化 K 个中心点 | |
| self.centroids = X[np.random.choice(X.shape[0], self.n_clusters, replace=False)] | |
| for _ in range(self.max_iter): | |
| # 分配样本到最近的中心点 | |
| labels = self._assign_clusters(X) | |
| # 更新中心点位置 | |
| self._update_centroids(X, labels) | |
| def _assign_clusters(self, X): | |
| # 计算样本到中心点的距离 | |
| distances = np.sqrt(((X - self.centroids[:, np.newaxis]) ** 2).sum(axis=2)) | |
| # 分配样本到最近的中心点 | |
| labels = np.argmin(distances, axis=0) | |
| return labels | |
| def _update_centroids(self, X, labels): | |
| # 更新中心点位置为所属簇的均值 | |
| for i in range(self.n_clusters): | |
| self.centroids[i] = X[labels == i].mean(axis=0) | |
| def predict(self, X): | |
| # 分配样本到最近的中心点 | |
| labels = self._assign_clusters(X) | |
| return labels | |
| kmeans = KMeans(n_clusters=3) | |
| kmeans.fit(X) | |
| labels = kmeans.predict(X) | |
| print(kmeans.centroids) |
其 3 个聚类中心坐标为:
| #kmeans.centroids | |
| [[5.77358491, 2.69245283], | |
| [6.81276596, 3.07446809], | |
| [5.006 , 3.428]] | |
| #centers | |
| [[6.82391304 3.07826087] | |
| [5.8 2.7] | |
| [5.00392157 3.40980392]] |
跟 2 中的 centers 差距不大。那么我们可视化结果看看。
| fig, axes = plt.subplots(1, 2, figsize=(16,8)) | |
| axes[0].scatter(X[:, 0], X[:, 1], c=labels, cmap='rainbow', | |
| edgecolor='k', s=150) | |
| axes[1].scatter(X[:, 0], X[:, 1], c=predicted_labels, cmap='rainbow', | |
| edgecolor='k', s=150) | |
| axes[0].set_xlabel('Sepal length', fontsize=16) | |
| axes[0].set_ylabel('Sepal width', fontsize=16) | |
| axes[1].set_xlabel('Sepal length', fontsize=16) | |
| axes[1].set_ylabel('Sepal width', fontsize=16) | |
| axes[0].tick_params(direction='in', length=10, width=5, colors='k', labelsize=20) | |
| axes[1].tick_params(direction='in', length=10, width=5, colors='k', labelsize=20) | |
| axes[0].set_title('Custom kmeans predicted', fontsize=18) | |
| axes[1].set_title('Sklearn Kmeans Predicted', fontsize=18) |
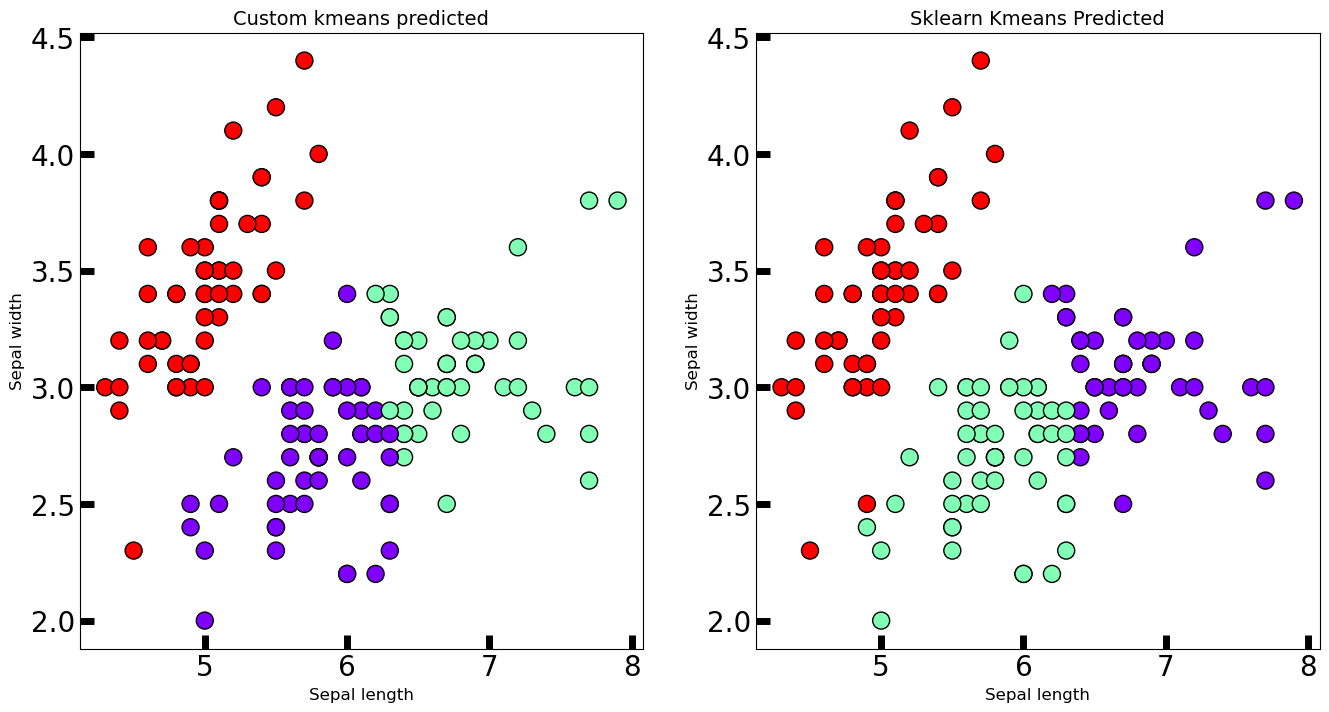
自己构建的 Kmeans 和 Sklearn 非常接近。说明我们搭建的 KMeans 是有效的,当然你也可以打印 labels 和 predicted_labels 来比较
Inference
[1] kmeans-clustering-from-scratch
正文完


