9. GlobalPointer 和 Efficient GlobalPointer 原理

1. GlobalPointer

GlobalPointer 来自于论文 GLOBAL POINTER: NOVEL EFFICIENT SPAN-BASED APPROACH FOR NAMED ENTITY RECOGNITION。也可阅读参考 1 来辅助理解。开源代码地址, Pytorch 版本地址。GlobalPointer 思路是:

1. 对于可以嵌套的 NER，我们如果假定要识别的文本长度为 $n$, 简单地假定只有一个实体，那么这个文本序列有多少个候选的实体呢？答案是 $n(n+1)/2$ 个。即长度为 $n$ 的序列有 $n(n+1)/2$ 个子序列
2. 在上面 $n(n+1)/2$ 个子序列选取真正的 $k$ 个实体，这就变成了 $n(n+1)/ 2 选 k$ 的多标签分类问题。
3. 进一步来讲，如果有 $m$ 种实体呢，就变成了 $m$ 个 $n(n+1)/ 2 选 k$ 的多标签分类问题

GlobalPointer 主要特点有：

1. 区间预测
2. ROPE 旋转式位置编码
3. 平衡的多标签分类损失

Approach

问题定义：NER 任务是从文本序列中抽取实体区间和识别其对应的类型。

假设 $S=[s_1, s_2, \cdots, s_m]$ 是文本序列，片段 $s[i:j]$ 是一个区间，NER 目标就是识别 $s\in E$, 其中 $E$ 是实体类型。

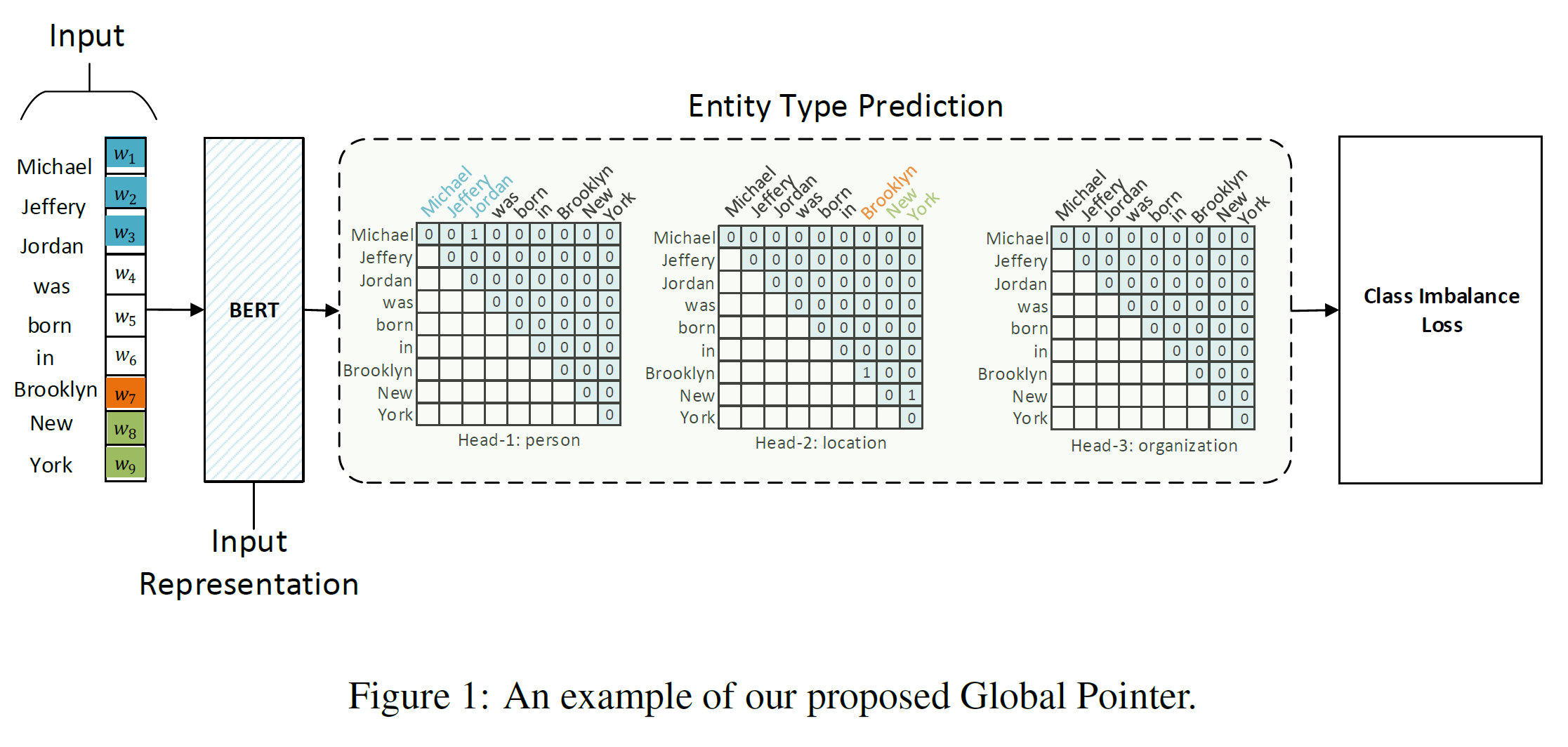
如上图 1 所示，Global Pointer 由两层构成，包括 token 表示 和区间预测。

1. token 表示：给定一个输入 n 个字符的句子 $X=[x_1, x_2, \cdots, x_n]$，经过 PLM 像 BERT 后能得到一个新的 token 的表示矩阵 $H \in \mathbb{R}^{n \times v}$, 这里 $v$ 是表示的维度。具体来说，将文本输入到 PLM 后得到 $n$ 个词 $v$ 维的表示，如 BERT 输入文本后取 last_hidden_state 就得到 $n \times 768$ 的矩阵，用式子表示为：

$$h_1, h_2, \cdots h_n = \text{PLM} (x_1, x_2, \cdots, x_n) \tag{1}$$

2. 区间预测：

接下来对获取到的句子表示 $H$, 计算其区间。作者使用两层前馈层来表示区间起始和结束的位置。
$$q_{i, \alpha} = W_{q, \alpha} h_{i} + b_{q, \alpha} \ k_{i, \alpha} = W_{q, \alpha} h_{i} + b_{q, \alpha} \tag{2}$$
其中 $q_{i, \alpha} \in \mathbb{R}^d, \ k_{i, \alpha} \in \mathbb{R}^d$ 是用来识别实体类型 $\alpha$ 的 token 的向量表示。具体来说，是对类型 $\alpha$ 片段 $s[i:j]$ 的起始和结束位置的表示为 $q_{i, \alpha}$ 和 $k_{i, \alpha}$。

那么片段 $s[i:j]$ 为 $\alpha$ 实体的分数可以计算为：
$$s_{\alpha}(i, j) = q_{i, \alpha}^Tk_{i, \alpha}\tag{3}$$
另外为了处理边界信息引入了 旋转式位置编码 Rotary Position Embedding。其实就是一个变换矩阵

$\boldsymbol{\mathcal{R}}_i$，满足 $\boldsymbol{\mathcal{R}}i^{\top}\boldsymbol{\mathcal{R}}_j = \boldsymbol{\mathcal{R}}{j-i}$。引入到式 3 有：

$$\begin{equation}s_{\alpha}(i,j) = (\boldsymbol{\mathcal{R}}i\boldsymbol{q}{i,\alpha})^{\top}(\boldsymbol{\mathcal{R}}j\boldsymbol{k}{j,\alpha}) = \boldsymbol{q}{i,\alpha}^{\top} \boldsymbol{\mathcal{R}}_i^{\top}\boldsymbol{\mathcal{R}}_j\boldsymbol{k}{j,\alpha} = \boldsymbol{q}{i,\alpha}^{\top} \boldsymbol{\mathcal{R}}{j-i}\boldsymbol{k}_{j,\alpha}\end{equation} \tag{4}$$
这样就注入了相对位置信息。

另外还引入了 多标签分类损失。

代码

Pytorch 实现如下代码：

1. qw,kw就是式 2 中的 $q_{i, \alpha} \in \mathbb{R}^d, \ k_{i, \alpha} \in \mathbb{R}^d$，实际上式 PLM 的 token 表示经过线性映射成 实体数目 x 2inner_dim(一般 bert 选 64)。然后拆分堆叠切片得到(batch_size, seq_len, ent_type_size, inner_dim)shape 的 tensor。
2. 对 qw,kw 引入 ROPE
3. 爱因斯坦求和得到分数 logits。

class GlobalPointer(nn.Module):
    def __init__(self, encoder, ent_type_size, inner_dim, RoPE=True):
        # encodr: RoBerta-Large as encoder
        # inner_dim: 64
        # ent_type_size: ent_cls_num
        super().__init__()
        self.encoder = encoder
        self.ent_type_size = ent_type_size
        self.inner_dim = inner_dim
        self.hidden_size = encoder.config.hidden_size
        self.dense = nn.Linear(self.hidden_size, self.ent_type_size * self.inner_dim * 2)
 
        self.RoPE = RoPE
 
    def sinusoidal_position_embedding(self, batch_size, seq_len, output_dim):
        position_ids = torch.arange(0, seq_len, dtype=torch.float).unsqueeze(-1)
 
        indices = torch.arange(0, output_dim // 2, dtype=torch.float)
        indices = torch.pow(10000, -2 * indices / output_dim)
        embeddings = position_ids * indices
        embeddings = torch.stack([torch.sin(embeddings), torch.cos(embeddings)], dim=-1)
        embeddings = embeddings.repeat((batch_size, *([1] * len(embeddings.shape))))
        embeddings = torch.reshape(embeddings, (batch_size, seq_len, output_dim))
        embeddings = embeddings.to(self.device)
        return embeddings
 
    def forward(self, input_ids, attention_mask, token_type_ids):
        self.device = input_ids.device
 
        context_outputs = self.encoder(input_ids, attention_mask, token_type_ids)
        # last_hidden_state:(batch_size, seq_len, hidden_size)
        last_hidden_state = context_outputs[0]
 
        batch_size = last_hidden_state.size()[0]
        seq_len = last_hidden_state.size()[1]
 
        # outputs:(batch_size, seq_len, ent_type_size*inner_dim*2)
        outputs = self.dense(last_hidden_state)
        #上一步已经转换为 bsxseq_lenxent_type_size*inner_dim*2
        #按照最后一个维度拆分成 ent_type_size 个 bs x seq_len inner_dim* 2 的 tensor
        outputs = torch.split(outputs, self.inner_dim * 2, dim=-1)
        # 将其堆叠成:(batch_size, seq_len, ent_type_size, inner_dim*2)
        outputs = torch.stack(outputs, dim=-2)
        # qw,kw:(batch_size, seq_len, ent_type_size, inner_dim)
        qw, kw = outputs[..., :self.inner_dim], outputs[..., self.inner_dim:]
        if self.RoPE:
            # pos_emb:(batch_size, seq_len, inner_dim)
            pos_emb = self.sinusoidal_position_embedding(batch_size, seq_len, self.inner_dim)
            # cos_pos,sin_pos: (batch_size, seq_len, 1, inner_dim)
            cos_pos = pos_emb[..., None, 1::2].repeat_interleave(2, dim=-1)
            sin_pos = pos_emb[..., None, ::2].repeat_interleave(2, dim=-1)
            qw2 = torch.stack([-qw[..., 1::2], qw[..., ::2]], -1)
            qw2 = qw2.reshape(qw.shape)
            qw = qw * cos_pos + qw2 * sin_pos
            kw2 = torch.stack([-kw[..., 1::2], kw[..., ::2]], -1)
            kw2 = kw2.reshape(kw.shape)
            kw = kw * cos_pos + kw2 * sin_pos
        # logits:(batch_size, ent_type_size, seq_len, seq_len)
        logits = torch.einsum('bmhd,bnhd->bhmn', qw, kw)
 
        # padding mask
        pad_mask = attention_mask.unsqueeze(1).unsqueeze(1).expand(batch_size, self.ent_type_size, seq_len, seq_len)
        logits = logits * pad_mask - (1 - pad_mask) * 1e12
 
        # 排除下三角
        mask = torch.tril(torch.ones_like(logits), -1)
        logits = logits - mask * 1e12
 
        return logits / self.inner_dim ** 0.5

参考

[1] GlobalPointer：用统一的方式处理嵌套和非嵌套 NER]

[2] Efficient GlobalPointer：少点参数，多点效果