14. HMM
1. HMM Background
机器学习大致分为两个派别，也就是频率派和贝叶斯派。
- 频率派，称为一门独立学科叫统计机器学习，核心问题是优化问题。主要有 3 个步骤：
- model，如 $f(w) = w^T + b$ 等。
- strategy，loss function。
- algorithm：GD/SGD/ 牛顿法 / 拟牛顿法。
- 贝叶斯派，衍生出概率图模型 PGM，最终是推断，即求解后验分布 $$p(z|x)$$，因为贝叶斯公式中，分母需要对所有状态空间进行积分，非常复杂，必须要解决这个数值积分问题，才能让贝叶斯网络能实际运用。这类方法代表有 MCMC，MCMC 发展出来的一系列数值积分方法把贝叶斯理论引入实际应用中。
Hidden Markov Model 隐马尔可夫模型 在概率图模型中的背景：
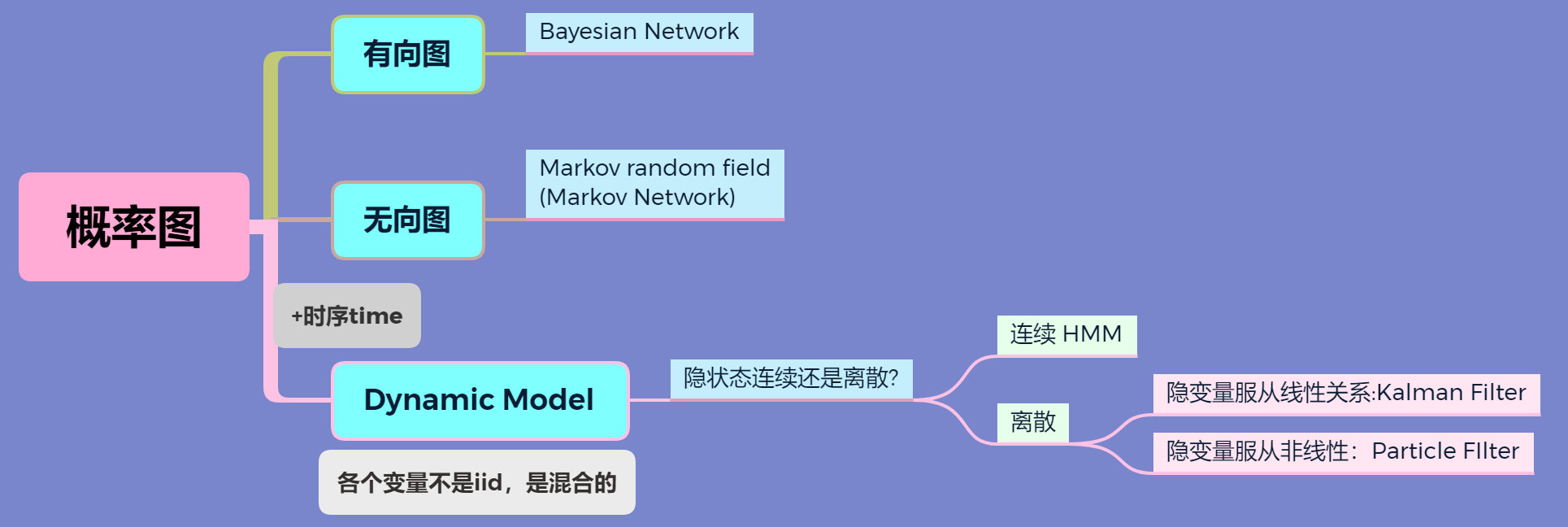
离散动态模型中 Kalman filter 和 Particle filter 将会在后续章节介绍。
2. HMM 算法整体介绍
1 个基本模型
隐马尔可夫模型是关于 时序 的概率模型 ，描述一个 隐藏的马尔可夫链 随机 生成不可观测的状态随机序列 ，再由各个 状态 生成一个观测从而产生 观测随机序列的过程。HMM 结构图如下：
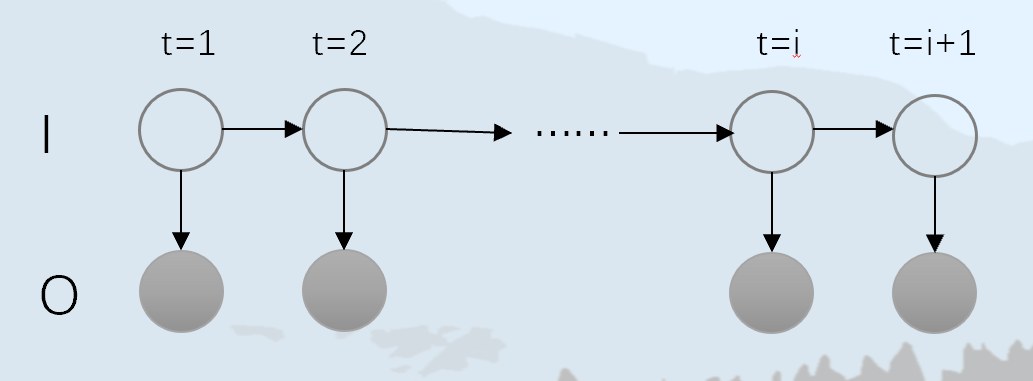
我们引入些符号来定义模型：
- 状态变量定义为：$I ={i_1, i_2, \cdots, i_t}$，如图中 I 这个序列。
- 观测变量定义为：$O={o_1, o_2, \cdots, o_t}$, 如图中 O 这个序列。
- 状态变量值的集合用 $Q = {q_1, q_2, \cdots, q_N}$, 就是说状态变量 $i_t$ 的值域，每个观测变量 $i_t$ 有 N 个状态可以取。
- 观测变量值的集合用 $V = {v_1, v_2, \cdots, v_M}$, 同样 V 是观测变量 $o_t$ 的值域。
- 状态转移矩阵 $A = [a_{ij}]{N\times N}$, $a{ij} = P(i_{t+1}=q_j| i_t=q_i)$
这里表示的就是状态变量从前一时刻 t 到下一时刻 t + 1 的概率值，就是 I 表示的空心圈状态序列从前往后变化的概率，根据上面定义的符号这是个 $N \times N$ 的矩阵。 - 发射矩阵(观测概率矩阵)$B =[b_j(k)]_{N \times M}, \quad b_j(k) = P(o_t =v_k|i_t=q_j)$, 这里表示的是在 t 时刻，从状态变量 $i_t=q_j$ 转移到观测变量 $o_t=v_k$ 的概率值，它是 $N \times M$ 的。
- 还有个初始状态概率 $\pi = {\pi_1, \pi_2, \cdots, \pi_N}$. 在 POS 中定义为每个词性出现在句首的概率。
这样，我们可以将 HMM 表示为一个三元组 $\lambda = (\pi, A, B)$。
2 个基本假设
另外，我们对于 HMM 有两个基本假设 李航——统计学习方法 P194：
- 齐次马尔可夫性假设 ，就是假设隐藏状态马尔可夫链在任意时刻只与前一时刻状态有关。
$$
P(i_t|i_{t-1}, o_{t-1}, \cdots, i_1, o_1) = P(i_t|i_{t-1}) \tag{1}
$$
就是满足该假设情况下，我们不用考虑隐状态和观察状态关系，也不需要考虑隐状态之前所有状态关系，只用计算前一时刻。 - 观测独立性假设：即任意时刻的观测只依赖该时刻马尔科夫链的状态，与其他观测和其他状态无关。
$$
P(o_t|i_t, o_{t-1}, i_{t-1}, \cdots, o_2, i_2, o_1, i_1) = P(o_t|i_t) \tag{2}
$$
从图上看，就是计算 t 时刻的观测状态概率只需要考虑该时刻的隐状态，不需要其它状态和节点。
3 个基本问题
- 概率计算问题：上面部分我们给定的 HMM $\lambda = (\pi, A, B)$ 和观测序列 $O$, 计算其在模型 $\lambda$ 下，序列 $O$ 出现的概率 $P(O|\lambda)$。具体来说，就是前向后向算法（接下来会具体介绍）。
- 学习问题: 已知观测序列 $O$，估计模型 $\lambda = (\pi, A, B)$ 参数，使得在该模型下观测序列概率 $P(O|\lambda)$ 最大。如 POS 中就是已知：
- 在有词性的初始状态(句首某个词性的概率)$\pi$，
- 当前词性转移到下一个词性的转移矩阵 $A$，
- 以及从该时刻的词性发射出具体某个词的发射矩阵 $B$ 的情况下，有具体的输出序列 $O$，因为已经生成了序列 $O$, 那么有观测序列概率 $P(O|\lambda)$ 最大。
- 具体求解 $\lambda$ 算法有：EM 算法和 Baum Welch 算法。
- Decoding 问题：求解后的模型 $\lambda = (\pi, A, B)$ 和观测序列 $O={o_1, o_2, \cdots, o_t}$, 求给定观测序列条件概率 $P(I|O)$ 最大的状态序列 $I = {i_1, i_2, \cdots, i_t}$。简单来说，就是在给定模型和观测序列后，求解隐状态序列。这分为预测和滤波：
- 预测问题：$P(i_{t+1}|o_1, \cdots, o_t) $, 也就是在已知当前观测变量情况下预测下一个状态，具体就是 Viterbi 算法。
- 滤波问题：$P(i_t|o_1, \cdots, o_t)$, 已知观测变量序列求 t 时刻隐变量。
接下来，我们逐个介绍 3 个问题的具体求解过程。
3. HMM 概率计算问题
由上节，我们知道概率计算问题就是在给定模型参数 $\lambda$ 情况下，求解 $P(O|\lambda)$，总的来说一下几种计算方法：
- 直接计算法 我们利用边缘概率和联合概率乘法公式有：
$$
P(O|\lambda) = \sum_I P(O, I | \lambda) = \sum_I P(O |I, \lambda)P(I |\lambda) \tag{3}
$$
其中 $\sum_I$ 表示所有隐状态序列求和，$ P(O|I, \lambda)$ 表示对应隐状态产生观测状态序列的概率，$P(I|\lambda)$ 是某个隐状态出现概率。
并且利用链式法则有：
$$
\begin{aligned}
P(I|\lambda)& = P(i_1, i_2\cdots , i_{T}|\lambda) \\
&=P(i_T|i_1, i_2\cdots , i_{T-1},\lambda) \cdots P(i_2|i_1, \lambda)P(i_1|\lambda)
\end{aligned}
\tag{4}
$$
而根据齐次马尔可夫假设式 1 有：
$$
P(i_T|i_1, i_2\cdots , i_{T-1},\lambda) = P(i_T|i_{T-1})=a_{i_{T-1}i_T }\tag{5}
$$
那么式 4 根据式 5 依次代入替换有：
$$
\begin{align}
P(I|\lambda)
&=P(i_T|i_1, i_2\cdots , i_{T-1},\lambda) \cdots P(i_2|i_1, \lambda)P(i_1|\lambda) \\
&=a_{i_{T-1}i_T }a_{i_{T-2}i_{T-1}}\cdots a_{i_{1}i_{2}} \pi_{i_1}\\
&=\pi_{i_1}\prod_{t=2}^T a_{i_{T-1}i_T }
\end{align}
\tag{6}
$$
对于公式 3 我们只要求计算出 $$P(O|I, \lambda)$$ 就可以了，利用观测独立性假设及联合概率有：
$$
\begin{align}
P(O|I, \lambda) &= P(o_1, o_2, \cdots, o_T|I, \lambda)\\
&= \prod_{i=1}^TP(o_t|I, \lambda)\\
&= \prod_{i=1}^T b_{i_t}(o_t)
\end{align}
\tag{7}
$$
现在公式 3 就等于：
$$
\begin{align}
P(O|\lambda) &= \sum_I P(O |I, \lambda)P(I |\lambda)\\
& = \sum_I \pi_{i_1}\prod_{t=2}^T a_{i_{T-1}i_T } \prod_{i=1}^T b_{i_t}(o_t) \\
& = \sum_{i_1} \sum_{i_2} \cdots \sum_{i_T} \pi_{i_1}\prod_{t=2}^T a_{i_{T-1}i_T } \prod_{i=1}^T b_{i_t}(o_t)
\end{align} \tag{8}
$$
公式 8 最后一步只是为了说明这将会有 $O(N^T)$ 个求和，总共计算复杂度为 $O(TN^T)$。在实际中是不可行的，为此我们引入前向 - 后向算法（forward-backward algorithm）。
- 前向 - 后向算法
前向算法
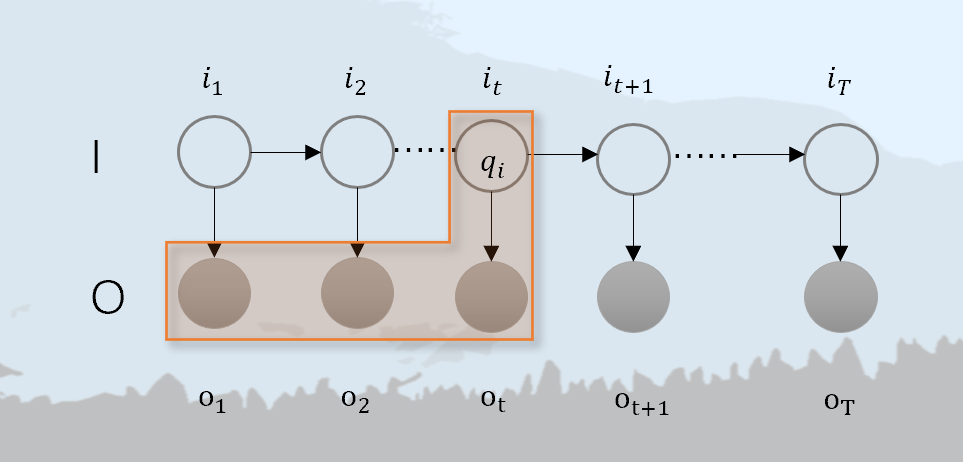
如上图橙色阴影所示，到时刻 t，隐状态变量为 $i_t=q_i$, 观测状态序列为 $o_1, o_2, \cdots, o_t$ 的概率，为前向概率，我们引入记号 $\alpha_t(i) = P(o_1, o_2, \cdots, o_t，i_t=q_i|\lambda)$ 来表示，更普遍一点表示为 $\alpha_T(i) = P(O,i_T= q_{T}|\lambda) $。
那么 $P(O|\lambda) = \sum_{i=1}^NP(O, i_t=q_i|\lambda)$ , 这表示时刻 t 时隐状态为 $q_i$, 观测状态序列为 $O$ 的前向概率。现在我们利用上述记号来推导:
$$
\begin{align}
\alpha_{t+1}(j) &= P(o_1, \cdots, o_t, o_{t+1}, i_{t+1}=q_j|\lambda)\\
&=\sum_{i=1}^N P(o_1, \cdots, o_t, o_{t+1}, i_{t+1}=q_j, i_t=q_i|\lambda)\\
&=\sum_{i=1}^N P(o_{t+1}|o_1, \cdots, o_t,i_{t+1}=q_j, i_t=q_i, \lambda) \cdot P(o_1, \cdots, o_t,i_{t+1}=q_j, i_t=q_i, \lambda) \\
&= \sum_{i=1}^N P(o_{t+1}|i_{t+1}=q_j) \cdot P(o_1, \cdots, o_t,i_{t+1}=q_j, i_t=q_i, \lambda) \quad \quad\text{式 2：观测独立性假设}\\
& =\sum_{i=1}^N P(o_{t+1}|i_{t+1}=q_j)\cdot P(i_{t+1}=q_j|o_1, \cdots, o_t, i_t=q_i, \lambda)\cdot P(o_1, \cdots, o_t, i_t=q_i| \lambda)\\
& =\sum_{i=1}^N b_j(o_{t+1}) a_{ij} \alpha_t(i)
\end{align} \tag{9}
$$
这表示，t 时刻隐状态为 $q_i$, 观测状态为 $O$ 乘以从隐状态 $i$ 转移到 $j$ 的概率再乘以由隐状态变量 $i_{t+1}=q_j$ 观测到 $o_{t+1}$ 的概率再求和。
下面借用 14 隐马尔可夫模型.pdf笔记中图来加强理解，对于前向算法来说，每个时刻 t 的输出状态都等于上一个隐状态分别计算概率再求和 。这实际上跟神经网络非常类似，就是前一状态值乘以权重。因为隐状态可取值为 $N$ 个，乘以对应概率，在对总共的序列长度 $T$ 求和，因此总的时间复杂度为 $O(TN^2)$，减少了大量计算。还可以看看 统计机器学习 P200 例 10.2。
后向算法
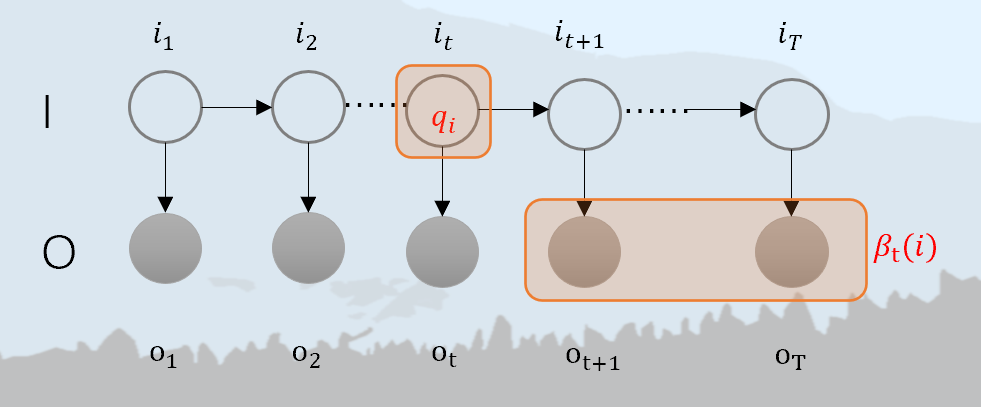
如上图所示，我们记 $\beta_t(i) = P(o_{t+1}, \cdots, o_T|i_t=q_i, \lambda)$, 就是 t 时刻在隐状态 $i_t=q_i$ 条件下，从 $t+1$ 到 $T$ 部分观测序列为 $o_{t+1}, \cdots, o_T$ 的概率，这就是后向概率。那么 $\beta_t(1) = P(o_{2}, \cdots, o_T|i_1=q_i, \lambda)$。若要计算 $P(O|\lambda)$，那么有：
$$
\begin{aligned} P(O|\lambda) &= P(o_1, o_2, \cdots, o_N|\lambda)\\&= \sum_{i=1}^NP(o_1, o_2, \cdots, o_N, i_1=q_i|\lambda)\quad \quad\text{边缘概率}\\ &= \sum_{i=1}^NP(o_1| o_2, \cdots, o_N, i_1=q_i,\lambda){\underbrace{P(i_1=q_i|\lambda)}{\pi_i} }\quad \text{条件概率}\\ &= \sum{i=1}^NP(o_1| o_2, \cdots, o_N, i_1=q_i,\lambda)\cdot P(o_2, \cdots, o_N, i_1=q_i|\lambda) \cdot \pi_i\\&=\sum_{i=1}^NP(o_1|i_1=q_i, \lambda) \cdot\beta_1(i)\cdot \pi_i\ \\&=\sum_{i=1}^Nb_i(o_1)\cdot\beta_1(i)\cdot \pi_i\\ &=\sum_{i=1}^N\pi_i\cdot b_i(o_1)\cdot \beta_1(i) \end{aligned} \tag{10}
$$
其中，$\pi_i$ 为某个初始状态的概率，$b_i(o_1)$ 第一个隐状态条件下生成第一个观测状态概率，$ \beta_1(i) $ 第 1 个观测状态确定后，生成后面观测序列的概率。另外，对于上述推导过程中，可以将 $\lambda$ 省去再思考推导过程。依旧借用 14 隐马尔可夫模型.pdf 中图如下，要确定输出观测序列，我们要知道初始隐状态概率，该隐状态转化为第一个观测状态概率，以及第一个观测条件下，生成后续观测序列的可能性只要将其相乘就可以了，分别对应下图蓝色，绿色，红色部分，并且可以看作一个信息传递过程。
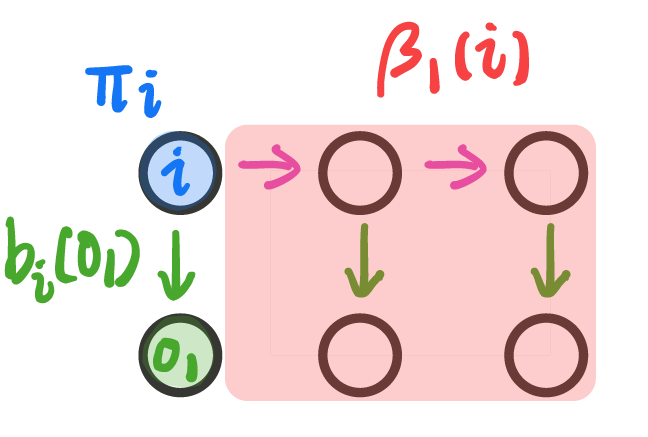
现在，我们要推广到 $\beta_t(i)$ 情况，这里省去 $\lambda$，方便推导表达式。
$$
\begin{align}
\beta_t(i) &= P(O|\lambda) \\&= P(o_{t+1}, o_{t+2}, \cdots, o_T|i_t=q_i)\\
&= \sum_{j=1}^N P(o_{t+1}, o_{t+2}, \cdots, o_T| i_{t+1}=q_j,i_t=q_i)P(o_{t+1}, o_{t+2}, \cdots, o_T, i_{t+1}=q_j|i_t=q_i) \quad{链式法则}\\
&= \sum_{j=1}^N P(o_{t+1}, o_{t+2}, \cdots, o_T| i_{t+1}=q_j,i_t=q_i)\cdot P(i_{t+1}=q_j|i_t=q_i) \quad{齐次假设} \\
&= \sum_{j=1}^N P(o_{t+1}, o_{t+2}, \cdots, o_T| i_{t+1}=q_j)\cdot a_{ij} \\
&= \sum_{j=1}^N P(o_{t+1}| o_{t+2}, \cdots, o_T, i_{t+1}=q_j)\cdot P(o_{t+2}, \cdots, o_T|i_{t+1}=q_j) \cdot a_{ij} \\
&= \sum_{j=1}^N b_{j}(o_{t+1}) \cdot \beta_{t+1}(j) \cdot a_{ij}\\
&= \sum_{j=1}^N a_{ij}\cdot b_{j}(o_{t+1}) \cdot \beta_{t+1}(j)
\end{align}\tag{11}
$$
跟上面一样的递推过程，依旧如下图的后向算法计算过程。
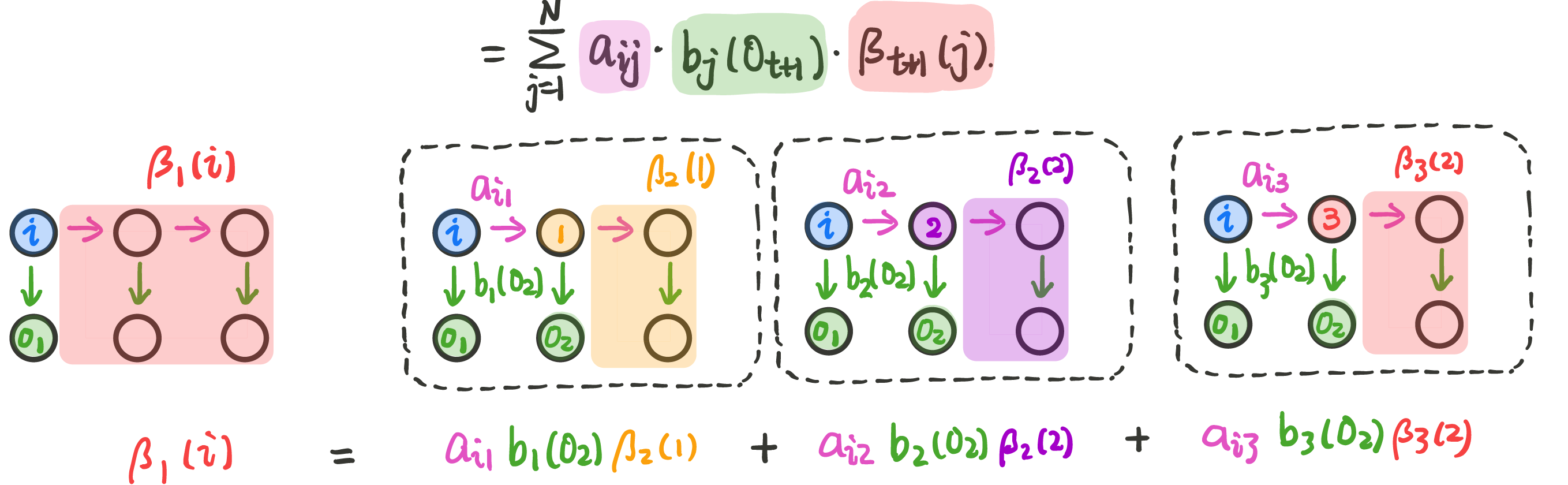
例：考虑盒子和球模型 $\lambda = (\pi,A,B)$，状态集合 $Q={1,2, 3}$，观测集合 $V={红, 白}$。(李航《统计学方法》P200)
$$
A = \begin{bmatrix}0.5 & 0.2 & 0.3\ 0.3& 0.5 & 0.2\ 0.2 & 0.3 & 0.5 \end{bmatrix}，B = \begin{bmatrix}0.5 & 0.5\ 0.4& 0.6\ 0.7 & 0.3 \end{bmatrix}，\pi = (0.2,0.4,0.4)^{T}
$$
设观测序列长度 $T=3$，观测序列为：$O=(红, 白, 红)$，求：$P(O|\lambda)$。代码来自 HMM-Evaluation.
import numpy as np
def forward(lamda, O):
'''
HMM 模型：概率计算问题——前向算法，李航《统计学方法》P177
step1:
t= 0 时刻，计算初值：alpha[t=1][j] = pai(j) * B[j][o1]
step2:
递推：t=1, 2, ..., T-1，计算 alpha[t][j]：alpha[t][j] = ∑(alpha[t-1][i] * A[i][j]) * B[j][ot]
step3:
计算：P(O|λ) = ∑alpha[T][j]
'''
A, B, pai = lamda # HMM 的参数：A, B, pai
N, M = B.shape # 状态集合 Q 的长度 N，观测集合 V 的长度 M
T = len(O) # 由观测序列得到 T 个时刻
'''HMM 的前向概率矩阵：T*N'''
alphas = np.zeros((T, N))
'''step1：t= 0 时刻，计算初值：alpha[t=0][j] = pai(j) * B[j][o1]'''
for j in range(N): # j 是当前状态
k = V.index(O[0]) # 第 Ot 个观测对应的 V 观测集合的位置 k:O[0]=V[k]
alphas[0][j] = pai[j] * B[j][k]
'''step2：递推：t=1, 2, ..., T-1，计算：alpha[t][j] = ∑(alpha[t-1][i] * A[i][j]) * B[j][Ot]'''
for t in range(1, T): # j 是当前状态
k = V.index(O[t]) # 第 Ot 个观测对应的 V 观测集合的位置 k:O[t]=V[k]
for j in range(N):
temp = 0
for i in range(N):
temp += alphas[t - 1][i] * A[i][j] # 计算：∑(alpha[t-1][i] * A[i][j])
alphas[t][j] = temp * B[j][k] # 计算：∑(alpha[t-1][i] * A[i][j]) * B[j][Ot]
'''step3：计算：P(O|λ) = ∑alpha[T][j]'''
prob = 0 # 求解 P(O|λ)
for j in range(N): # j 是当前隐状态
prob += alphas[T - 1][j]
return prob
if __name__ == '__main__':
'''状态集合：Q = {q1, q2, ..., qN}'''
Q = ['盒子 1', '盒子 2', '盒子 3']
'''观测集合：V = {v1, v2, ..., vM}'''
V = ['红', '白']
'''
状态转移概率矩阵：A = [aij]，其中 aij = P(it+1=qj | it=qi)
A: shape N * N (盒子之间互相转换)
'''
A = np.array([[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]])
'''
观测概率矩阵：B=[bj(k)]，其中 bj(k) = P(ot=vk | it=qj)
B: shape N * M (N 个盒子 M 个观测)
'''
B = np.array([[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]])
'''初始状态概率向量：pai = P(i1=qi)：第一次出现每个盒子的概率分布'''
pai = np.array([0.2, 0.4, 0.4])
'''随机序列 1——观测序列：O = {o1, o2, ..., oT}'''
'''随机序列 2——状态序列（隐序列，叠加态的黑盒子）：I = {i1, i2, ..., iT}'''
O = np.array(['红', '白', '红'])
'''前向算法计算：P(O|λ)'''
P_O_or_lamda = forward(lamda=[A, B, pai], O=O)
print('通过 HMM 前向算法计算概率：\n 观测序列：{} 出现的概率 P(O|λ) = {:.4f}'.format(O, P_O_or_lamda))4. Viterbi 算法
隐马尔可夫模型中的维特比算法，用于解码给定的观测序列和模型参数，得到最有可能的隐藏状态序列。
该代码实现了 HMM 模型的三个基本问题：
- 概率计算问题：给定模型参数和观测序列，计算这个序列出现的概率。
- 学习问题：给定观测序列，估计模型参数，使得这个观测序列出现的概率最大。
- 解码问题：给定模型参数和观测序列，找到最有可能的隐藏状态序列。
具体来说，该代码实现了维特比算法（Viterbi algorithm），用于解码问题，即在给定模型参数和观测序列的情况下，找到最有可能的隐藏状态序列。
代码中的 viterbi 函数接受两个参数：一个观测序列 obs，一个 HMM 模型 model。model 包括三个参数：初始状态概率向量 model['start_prob']、状态转移概率矩阵 model['trans_prob']、观测概率矩阵 model['emit_prob']。
函数中的主要步骤是：
- 初始化：将起始概率向量
model['start_prob']和第一个观测值对应的观测概率向量model['emit_prob'][:, obs[0]]相乘，得到一个长度为状态数的向量probs，并将其作为维特比算法的第一个状态。 - 递推：对于观测序列中的每个观测值，根据当前状态向量
probs和状态转移概率矩阵model['trans_prob']，计算出下一个状态向量next_probs，并将其作为下一次迭代的当前状态向量。 - 回溯：在所有观测值都处理完之后，根据每个状态向量的最大值以及指向最大值的箭头，得到最有可能的隐藏状态序列。
import numpy as np
# Define the Viterbi algorithm
def viterbi(obs, states, obs_symbols, initial_prob, transitions, emissions):
"""
viterbi algorithm to get best_path and prob_best_path
:param obs: 要已经划分完毕的标注的句子, split/tokenized
:param states: 词性的所有状态
:param obs_symbols: 所有词的列表
:param initial_prob: 初始概率矩阵
:param transitions: 转移矩阵
:param emissions: 发射矩阵
:return:
"""
# Define the T x N matrix for probabilities
T = len(obs) #要标注的句子长度
N = len(states) #pos tag 长度
probs = np.zeros((T, N)) #保存句子每个词到指定 tag 的概率
# Define the T x N matrix for pointers to backtrack
pointers = np.zeros((T, N), dtype=int)
# Calculate probabilities and pointers for the first observation
# 初始化第一个词对应词性 prob
obs_index = obs_symbols.index(obs[0])
probs[0] = np.multiply(initial_prob, emissions[:, obs_index])
# Iterate over the remaining observations
for t in range(1, T):
#输入句子的词对应在观察序列列表的索引
obs_index = obs_symbols.index(obs[t])
for s in range(N):
#第 t 个词前一个词的概率乘以转移概率. 这里从 1 循环到 T 句子长度的过程中都是拿前面一个
#来获得当前词性的概率, 已经初始化得到 0，那么 1 就是 probs[0] *transitions[:, s]
#迭代获取所有当前词性的概率
temp_probs = np.multiply(probs[t - 1], transitions[:, s])
#取最大概率的 index
max_prob_index = np.argmax(temp_probs)
#那么对应最大概率 = 发射矩阵矩阵中词 * 当前词性最大概率
probs[t, s] = emissions[s, obs_index] * temp_probs[max_prob_index]
#为解码取路径保存索引来 这个索引表示 t 时刻对应上一时刻的最大的 prob 连接的索引
pointers[t, s] = max_prob_index
# Find the best path
#最后一行的最大的索引
best_path = [np.argmax(probs[-1])]
for t in range(T - 1, 0, -1):
best_path.append(pointers[t, best_path[-1]])
best_path.reverse()
# Calculate the probability of the best path
prob_best_path = np.max(probs[-1])
return best_path, prob_best_path
# Example usage
obs = ['walk', 'shop', 'clean']
# Define states
states = ('Rainy', 'Sunny')
# Define observation symbols
obs_symbols = ('walk', 'shop', 'clean')
# Define initial probabilities
initial_prob = np.array([0.6, 0.4])
# Define transition matrix
transitions = np.array([[0.7, 0.3],
[0.4, 0.6]])
# Define emission matrix
emissions = np.array([[0.1, 0.4, 0.5],
[0.6, 0.3, 0.1]])
best_path, prob_best_path = viterbi(obs, states, obs_symbols, initial_prob, transitions, emissions)
print("Best path:", [states[i] for i in best_path])
print("Probability of the best path:", prob_best_path)Inference
[1] HMM 前向与后向算法
[3] HMM-Evaluation
