1. Precision,Recall,F1-score 解释
这些名词都建立在混淆矩阵 confusion matirx 之上,如下所示:
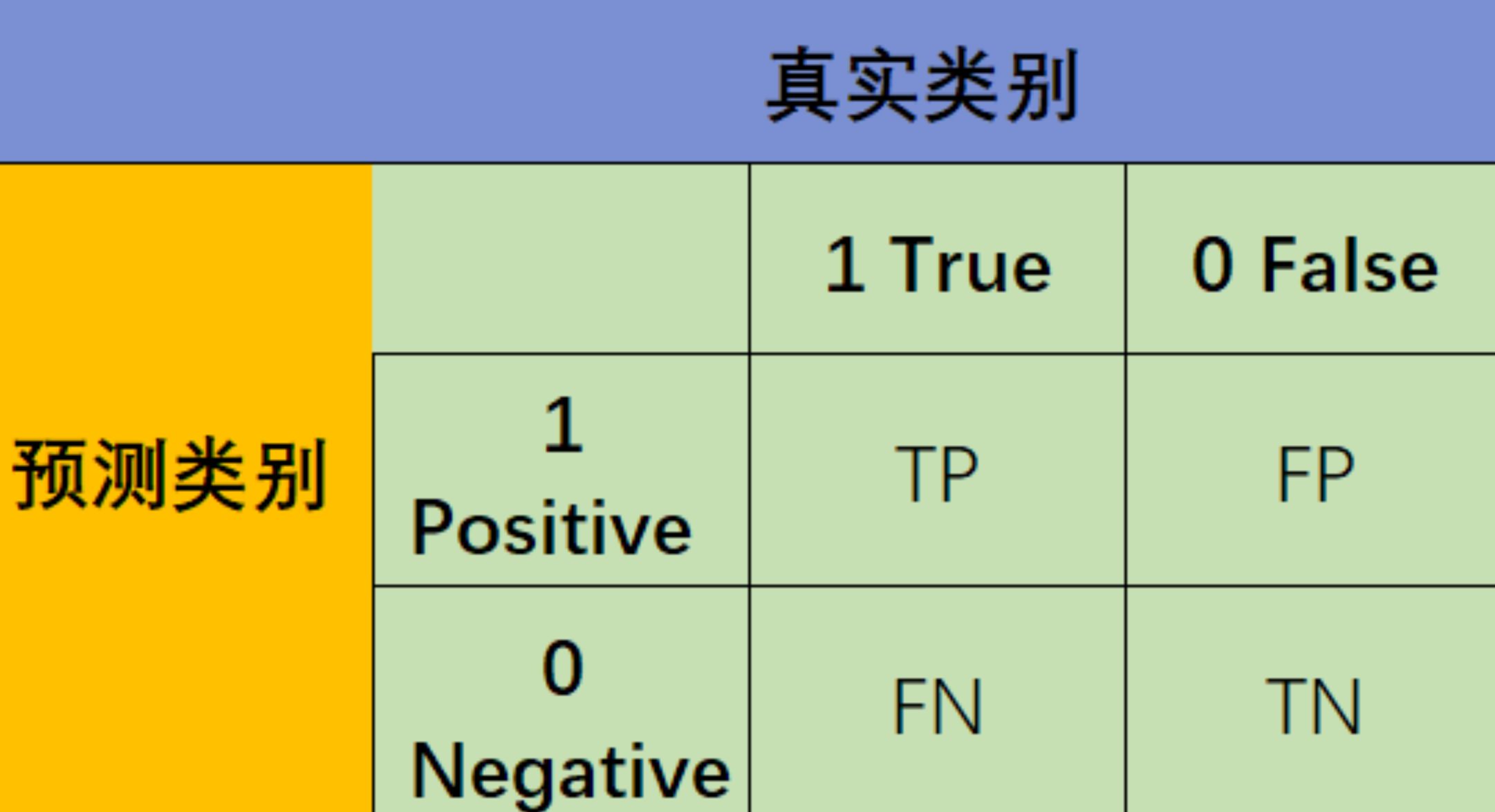
| TP 真正例 | FN 假反例 | |
| FP 假正例 | TN 真反例 |
查准率和查全率分别为:
P:precision=TPTP+FPR:recall=TPTP+FN
- 查准率 precision:就是找到的正例中有多少是真正的正例(实际上是比率),就等于真正的正例 / 所有预测的正例
- 查全率 recall:又叫召回率, 就是在找到的真正例在所有原始样本中的比例,(所有原始样本数目 = 真正例和反例和),在混淆矩阵中就是 TP+FN,实际上就等于真正的正例 / 所有原始样本数。更通俗地说,把目标样本找全了没,而 查准率 是你找准了多少正样本。
| import numpy as np | |
| from sklearn import metrics | |
| ## 给定的真实 y 和 预测 pred | |
| y = np.array([1, 0, 0, 0, 1, 0, 1, 0, 0, 1]) | |
| pred = np.array([0.9, 0.4, 0.3, 0.1, 0.35, 0.6, 0.65, 0.32, 0.8, 0.7]) | |
| def recall(true, pred): | |
| tp = np.sum(np.logical_and(true==1, pred==1)) | |
| fn = np.sum(np.logical_and(true==1, pred==0)) | |
| recall_score = tp/(tp+fn) | |
| return recall_score | |
| def precision(true, pred): | |
| tp = np.sum(np.logical_and(true==1, pred==1)) | |
| fp = np.sum(np.logical_and(true==0, pred==1)) | |
| precision_score = tp/(tp+fp) | |
| return precision_score | |
| recall_score = recall(y, pred>=0.5) | |
| print(recall_score) | |
| sk_recall_score = metrics.recall_score(y, pred>=0.5) | |
| print(sk_recall_score) | |
| precision_score = precision(y, pred>=0.5) | |
| print(precision_score) | |
| sk_precision_score = metrics.precision_score(y, pred>=0.5) | |
| print(sk_precision_score) |
而 F1-score 是:它是 P 和 R 的调和平均:
F1=21/P+1/R=2×P×RP+R
Macro-F1 和 Micro-F1
- Macro-F1 和 Micro-F1 是相对于多标签分类而言的。
- Micro-F1,计算出所有类别总的 Precision 和 Recall,然后计算 F1。
- Macro-F1,计算出每一个类的 Precison 和 Recall 后计算 F1,最后将 F1 平均。
代码示例:
| def f1(actual, predicted, label): | |
| """A helper function to calculate f1-score for the given `label`""" | |
| # F1 = 2 * (precision * recall) / (precision + recall) | |
| tp = np.sum((actual==label) & (predicted==label)) | |
| fp = np.sum((actual!=label) & (predicted==label)) | |
| fn = np.sum((predicted!=label) & (actual==label)) | |
| precision = tp/(tp+fp) | |
| recall = tp/(tp+fn) | |
| f1 = 2 * (precision * recall) / (precision + recall) | |
| return f1 | |
| def f1_macro(actual, predicted): | |
| # `macro` f1- unweighted mean of f1 per label | |
| return np.mean([f1(actual, predicted, label) | |
| for label in np.unique(actual)]) | |
| actual = np.array(["A","A","B","C","C"]) | |
| predicted = np.array(["A","B","B","C","C"]) | |
| label=np.array(["A","B","B","C","A"]) | |
| print(f1(actual, predicted, label)) | |
| print(f1_macro(actual, predicted)) | |
| ====================================================== | |
| 0.8571428571428571 | |
| 0.7777777777777777 | |
Keras 实现 Keras Macro F1-Score Implementation:
| import tensorflow as tf | |
| import keras.backend as K | |
| def f1(y_true, y_pred): | |
| y_pred = K.round(y_pred) | |
| tp = K.sum(K.cast(y_true*y_pred, 'float'), axis=0) | |
| # tn = K.sum(K.cast((1-y_true)*(1-y_pred), 'float'), axis=0) | |
| fp = K.sum(K.cast((1-y_true)*y_pred, 'float'), axis=0) | |
| fn = K.sum(K.cast(y_true*(1-y_pred), 'float'), axis=0) | |
| p = tp / (tp + fp + K.epsilon()) | |
| r = tp / (tp + fn + K.epsilon()) | |
| f1 = 2*p*r / (p+r+K.epsilon()) | |
| f1 = tf.where(tf.is_nan(f1), tf.zeros_like(f1), f1) | |
| return K.mean(f1) | |
| import numpy as np | |
| from sklearn.metrics import f1_score | |
| # Samples | |
| y_true = np.array([[1,1,0,0,1], [1,0,1,1,0], [0,1,1,0,0]]) | |
| y_pred = np.array([[0,1,1,1,1], [1,0,0,1,1], [1,0,1,0,0]]) | |
| print('Shape y_true:', y_true.shape) | |
| print('Shape y_pred:', y_pred.shape) | |
| # Results | |
| print('sklearn Macro-F1-Score:', f1_score(y_true, y_pred, average='macro')) | |
| print('Custom Macro-F1-Score:', K.eval(f1(y_true, y_pred))) | |
| ========================================================== | |
| Shape y_true: (3, 5) | |
| Shape y_pred: (3, 5) | |
| sklearn Macro-F1-Score: 0.5999999999999999 | |
| Custom Macro-F1-Score: 0.5999999 |
2.ROC 和 AUC
Receiver operating characteristic wiki 有全面的介绍。AUC(Area Under the ROC Curve)指标是评估二分类模型的另一个重要指标,它的计算方法是先画出 ROC 曲线,然后计算曲线下面积。ROC 曲线的横轴是 False Positive Rate(FPR),表示实际为负类的样本中被预测为正类的比例;纵轴是 True Positive Rate(TPR),表示实际为正类的样本中被预测为正类的比例。AUC 的取值范围在 0.5 和 1 之间,越接近 1 表示模型的性能越好。
在使用这两个指标进行模型评估时,通常会计算它们在验证集或测试集上的平均值作为模型的最终指标,以便于不同模型之间的比较。
ROC 曲线又称,“受试者工作特征——ReceiverOperating Characteristic”。与 P_R 曲线使用 P, R 为纵横坐标不同,ROC 使用的是:(以 FPR 为 x 轴,TPR 为 y 轴画图,就得到了 ROC 曲线)。如上图所示,在二元分类任务中,一般将正例样本预测为正例称为 True Positive(TP),将负例样本预测为正例称为 False Positive(FP),将负例样本预测为负例称为 True Negative(TN),将正例样本预测为负例称为 False Negative(FN)。
- 纵轴:
TPR True Positive Rate简称 TPR,正确分类的正样本在所有正例样本中占比,即表示实际为正例并被正确地预测为正例的样本占所有实际为正例样本的比例,其计算公式跟 Recall 一样。也称为 Recall 或 Sensitivity。 - 横轴:
FPR False Positive Rate简称 FPR,FP 在所有负例样本中占比,也可以说是所有负例样本预测为正例的,即表示实际为负例但被错误地预测为正例的样本占所有实际为负例样本的比例,即:。(误分嘛,把正的分类成负的——FP, 把负的分类成正的——TN。
计算公式为:
TPR=TPTP+FNFPR=FPTN+FP
对照上面混淆矩阵图示,
- TPR 就是针对 1 这列计算,TP 除以 1 这一列的和
- FPR 就是针对 0 这列计算,FP 除以 0 这一列的和
将 同一模型每个阈值 的 (FPR, TPR) 座标都画在 ROC 空间里,就成为 特定模型的 ROC 曲线
ROC 曲线下方的面积(英语:Area under the Curve of ROC (AUC ROC)),其意义是:
- 因为是在 1 ×1 的方格里求面积,AUC 必在 0~1 之间。
- 假设阈值以上是阳性,以下是阴性;
- 若随机抽取一个阳性样本和一个阴性样本,分类器 正确判断 阳性样本的值高于阴性样本之 几率 =AUC=AUC[1]。
- AUC 物理意义:AUC 是 area under curve 的缩写,它定义为 ROC 曲线下的面积。它的物理意义是:随机选出一对正负样本,模型对正样本的打分大于对负样本打分的概率。通常用于衡量一个分类模型把真正的正样本排在负样本前面的能力,能力越强则 AUC 越高。AUC 的优点在于不受正负样本分布的影响。简单说:AUC 值越大的分类器,正确率越高。
Inference
[1] 一文读懂分类算法常用评价指标
[2] 精确率、召回率、F1 值、ROC、AUC 各自的优缺点是什么?
[4] 评估分类模型
[5] F1 分数 (F1 Score) 详解及 tensorflow、numpy 实现
[6] computing-macro-average-f1-scor
[7] AUC 的面试


