Abstract
我们介绍一种稀疏专家混合 (SMoE) 语言模型 Mixtral 8x7B。Mixtral 的架构与 Mistral 7B 相同，不同之处在于每个层由 8 个前馈块（即专家）组成。对于所有的 token，每一层的路由器网络都会选择两个专家来处理当前状态并结合他们的输出。尽管每个 token 只看到两个专家，但在每个时间步，选定的专家可以不同。因此，每个 token 可以访问 47B 的参数，但在推理过程中只使用 13B 的活动参数。Mixtral 使用 32k token 的上下文进行训练，其性能超越或匹敌 Llama 2 70B 和 GPT-3.5，覆盖了所有评估的基准测试。特别是在数学、代码生成和多语言基准测试上，Mixtral 远超 Llama 2 70B。我们还提供了一个经过微调的模型，用于遵循指令，即 Mixtral 8x7B-Instruct 模型，该模型在人类基准测试中超过了 GPT-3.5 Turbo、Claude-2.1、Gemini Pro，以及 Llama 2 70B- chat model。基础模型和 instruct 模型都已经在 Apache 2.0 许可下发布。
Code: https://github.com/mistralai/mistral-src
Webpage: https://mistral.ai/news/mixtral-of-experts/
最主要的是 FFN 替换成了 MOE 如 opencompass 图示(Inference 1)：
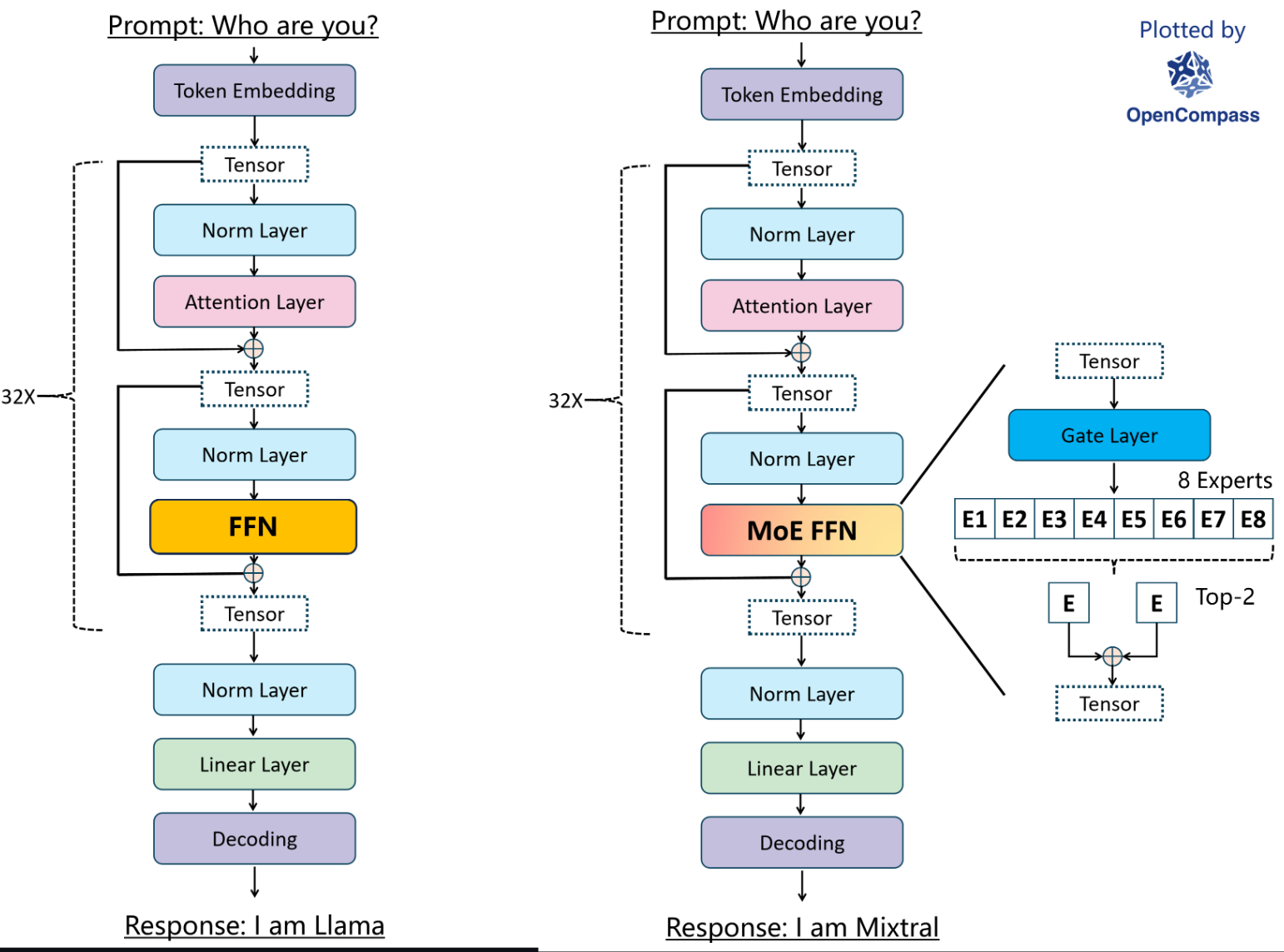
- 在所有测试集上优于 llama2 1B 效果。
- 大多数测试集上优于 llama1 34B 效果。
- 代码能力接近 codellama 7B，在非代码测试集上表现出色。
- 利用 GQA（grouped query attention）实现更快的推理速度。
- 使用 SWA（Sliding Window Attention）能以小显存代价处理更长的文本序列。
1. Introduction
Mixtral 是一个稀疏的专家混合网络。它是一个 decoder-only 模型，其中前馈层从 8 组不同的参数组中选择。在每一层，对于每个 token，一个路由器网络选择这些组中的两个（“专家”）来处理 token 并将它们的输出加在一起。这种技术在控制成本和延迟的同时增加了模型的参数数量，因为模型每个 token 只使用总参数集的一部分。
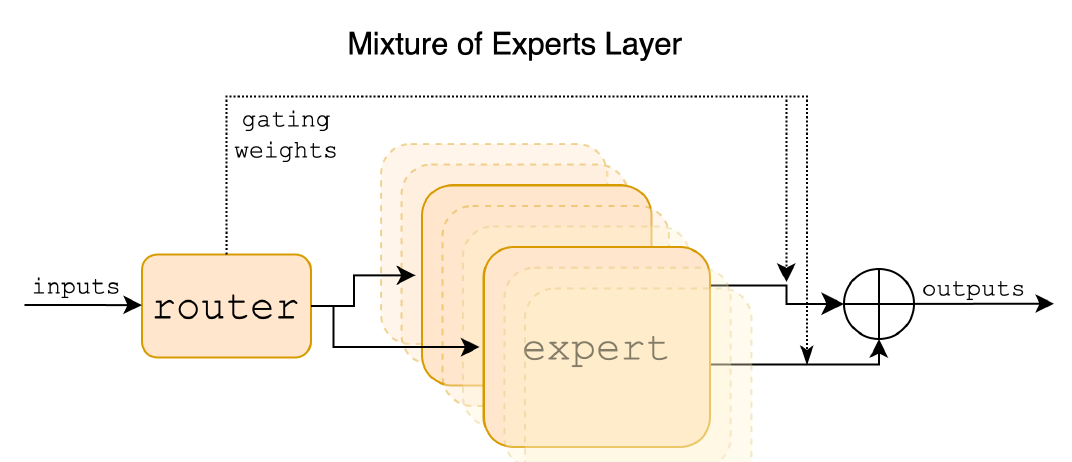
图 1：Mixture of Experts Layer。每个输入向量由路由器分配给 8 个专家中的 2 个。该层的输出是两个选定专家的输出的加权和。在 Mixtral 中，一个专家是标准的前馈块，就像在普通的 Transformer 架构中一样。
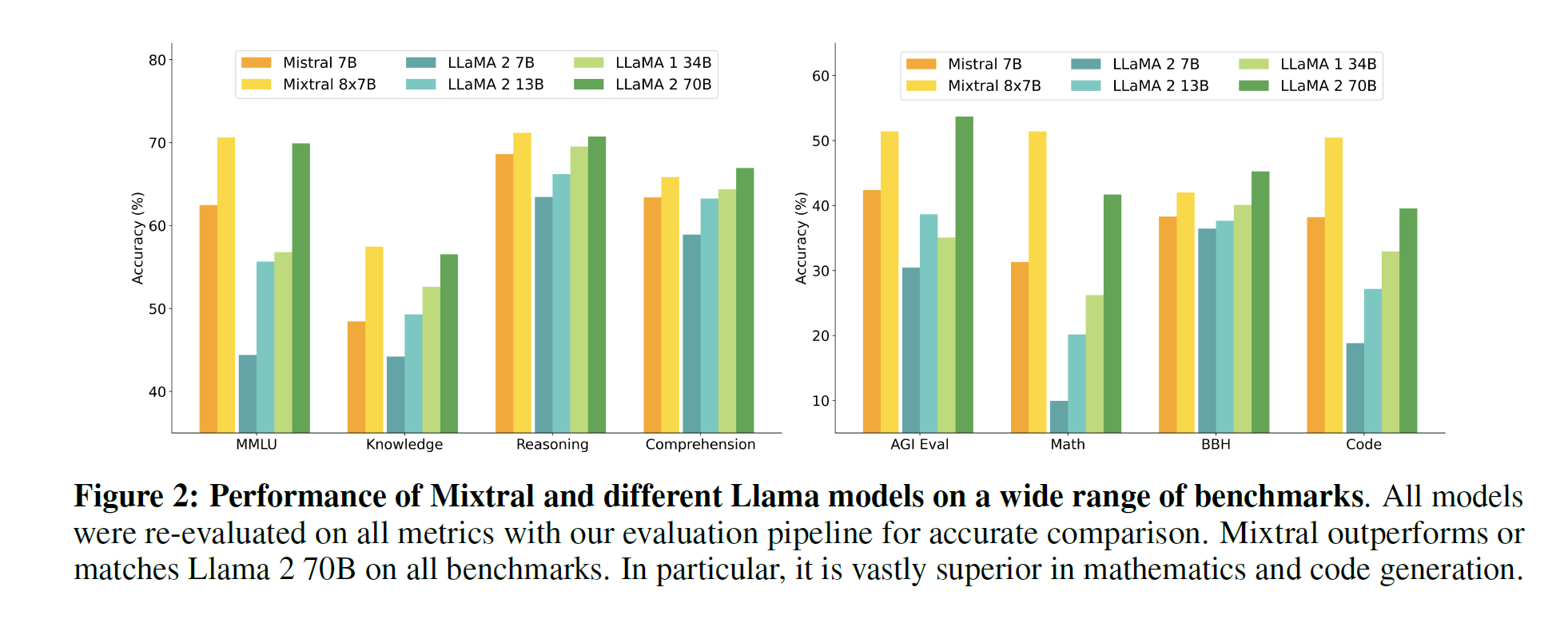
Mixtral 在数学、代码生成和需要多语言理解的任务上表现出优越的能力，显著优于 Llama 2 70B。实验表明，无论序列长度和信息在序列中的位置如何，Mixtral 都能够成功地从其 32k 令牌的上下文窗口中检索信息。
我们还介绍了 Mixtral 8x7B – Instruct，这是一个经过微调的聊天模型，使用监督微调和直接优选优化来遵循指令。在人类评估基准测试中，其性能明显超过了 GPT-3.5 Turbo、Claude-2.1、Gemini Pro 和 Llama 2 70B – chat model。Mixtral – Instruct 在 BBQ 和 BOLD 等基准测试中也表现出了减少的偏见和更平衡的情感特征。
我们在 Apache 2.0 许可下发布了 Mixtral 8x7B 和 Mixtral 8x7B – Instruct，免费供学术和商业用途使用，确保了广泛的可访问性和多样化应用的潜力。为了让社区能够通过完全开源的堆栈运行 Mixtral，我们向 vLLM 项目提交了更改，该项目整合了 Megablocks CUDA 核心以进行高效推理。Skypilot 还允许在云中的任何实例上部署 vLLM 端点。
2. Architectural details
2.1 Sparse Mixture of Experts
给出了专家混合层（图 1）的简洁概述。要获取更深入的概述，请参阅[12]。对于给定的输入 x，MoE 模块的输出由专家网络输出的加权和决定，其中权重由门控网络的输出给出。也就是说，给定 n 个专家网络 ${E_0, E_i, \cdots E_{n-1}}$，专家层的输出由以下公式给出：
$$
\sum_{i=0}^{n-1} G(x)_i \cdot E_i(x) \tag{1}
$$
在这里，$G(x)_i$ 表示第 $i$ 个专家的门控网络的 $n$ 维输出，$E_i(x)$ 是第 $i$ 个专家网络的输出。如果门控向量是稀疏的，我们可以避免计算 gate 值为零的专家的输出。实现 $G(x)$的方式有很多种，但一种简单且高效的方法是对线性层的 Top-K logits 取 softmax。我们使用:
$$
G(x) := \text{Softmax} (\text{TopK} (x·W_g)), \tag{2}
$$
其中，如果 $ℓ_i$ 在 $\text{logits} \ ℓ \in \mathbb{R}^n$ 的 top- K 坐标中，那么 $(\text{TopK}(ℓ))_i:= ℓ_i$；否则，$(\text{TopK} (ℓ))_i:=−∞$。
import torch
import torch.nn as nn
from simple_parsing.helpers import Serializable
from dataclasses import dataclass
from typing import List
@dataclass
class MoeArgs(Serializable):
num_experts: int
num_experts_per_tok: int
class FeedForward(nn.Module):
def __init__(self, args: MoeArgs):
super().__init__()
self.linear = nn.Linear(args.dim, args.dim)
def forward(self, x):
return self.linear(x)
class MoeLayer(nn.Module):
def __init__(self, experts: List[nn.Module], gate: nn.Module, moe_args: MoeArgs):
super().__init__()
assert len(experts) > 0
self.experts = nn.ModuleList(experts)
self.gate = gate
self.args = moe_args
def forward(self, inputs: torch.Tensor):
gate_logits = self.gate(inputs)
weights, selected_experts = torch.topk(gate_logits, self.args.num_experts_per_tok)
weights = nn.functional.softmax(weights, dim=1, dtype=inputs.dtype)
results = torch.zeros_like(inputs)
for i, expert in enumerate(self.experts):
batch_idx, nth_expert = torch.where(selected_experts == i)
results[batch_idx] += weights[batch_idx, nth_expert, None] * expert(inputs[batch_idx]
)
return results可以看到，weights, selected_experts = torch.topk(gate_logits, self.args.num_experts_per_tok)就是门控网络 gate 获取的权重和对应的专家，然后在输出是将每个专家的输出和权重相乘得到。在 ff 中运行例子如下：
@dataclass
class Args(Serializable):
dim: int = 512
moe: MoeArgs = MoeArgs(num_experts=8, num_experts_per_tok=2)
args = Args()
moe_layer = MoeLayer(experts=[FeedForward(args=args) for _ in range(args.moe.num_experts)],
gate=nn.Linear(args.dim, args.moe.num_experts, bias=False),
moe_args=args.moe,
)
# Run the MoE layer
input_tensor = torch.randn(10, args.dim)
output = moe_layer(input_tensor)
print(output.shape) # Output: torch.Size([10, 512])K 的值 ——每个 token 使用的专家数量，这 是一个超参数，用来调节处理每个 token 所使用的计算量。
当保持 K 固定并增加 n 的值时，模型的参数数量会增加。这是因为 n 代表的是模型中可供选择的专家网络总数。每一个专家网络都有自己的参数，因此当你增加专家网络的数量时，你也就增加了模型的总参数数量。然而，尽管模型的总参数数量增加了，但是由于每次只选择 K 个专家网络进行计算，所以计算成本在实际效果上保持不变。
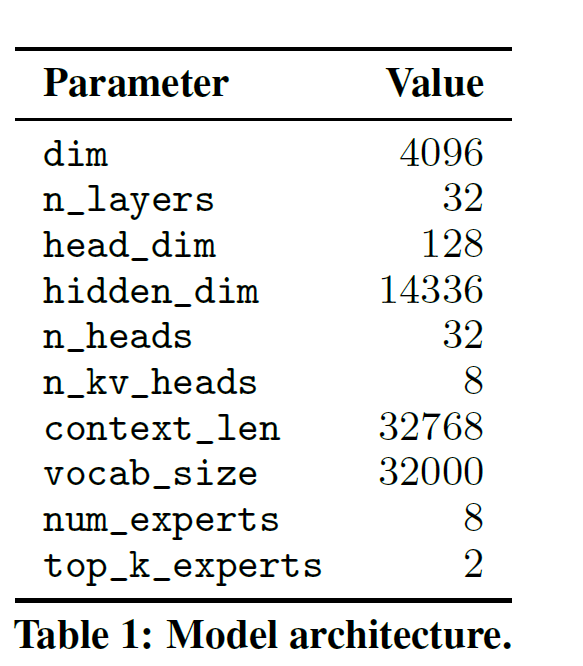
在 Transformer 模型中，MoE 层独立地应用于每个令牌，并替换了 Transformer 块的前馈（FFN）子块。对于 Mixtral，我们使用与专家函数 $E_i(x)$ 相同的 SwiGLU 架构，并设置 K =2。这意味着每个 token 都被路由到具有不同权重集的两个 SwiGLU 子块。
综合考虑这一切，输入 token $x$ 的输出 $y$ 是这样计算的：
$$
y = \sum_{i=0}^{n-1} \text{Softmax}(\text{Top}2(x \cdot W_g))_i \cdot \text{SwiGLU}_i(x) \tag{3}
$$
评测效果
