1. DDPM 前向过程
DDPM 是 Denoising Diffusion Probabilistic Models 的简称,即降噪扩散概率模型,论文地址 。本文主要参考了 What are Diffusion Models? 和扩散模型之 DDPM,都写得非常好。公式序号没 a 的是原文,有 a 的是本文排序,方便对照。
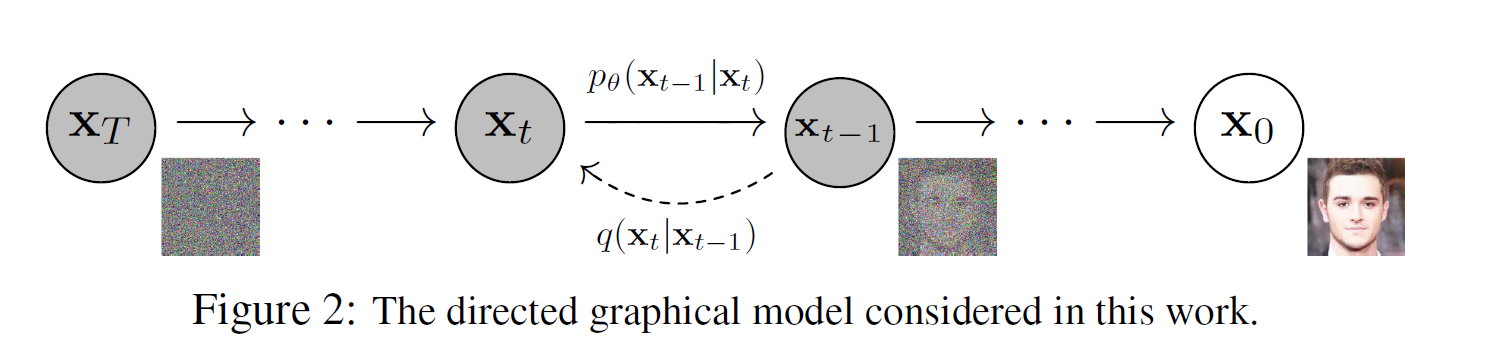
q(x1:T∣x0):=T∏t=1q(xt∣xt−1) q(xt∣xt−1):=N(xt;√1−βtxt−1,βtI)
公式 2 表示了在扩散过程中,如何从时间步长 t−1 的数据 xt−1 生成时间步 t 的数据 xt。逐步解释如下:
- q(x1:T|x0) 表示从初始数据 x0 出发,生成整个序列 x1:T 的概率分布模型。–
- 这个序列分布被分解为 T 个条件分布的乘积:q(xt|xt−1) 表示在给定前一步 xt−1 的条件下,生成当前步 xt 的条件概率分布。每个条件分布 q(xt|xt−1) 被参数化为一个高斯分布:
- 均值是前一步 xt−1 被重新缩放的值:√1−βt⋅xt−1
- 方差是 βt⋅I,其中 βt 是一个预先设定的扩散程度参数,I 是单位矩阵。
- 因此,生成 xt 的过程是:
- 重新缩放前一步 xt−1
- 添加以 βt 为方差的高斯噪声。随着 t 的增加,这个过程会使得数据 xt 逐渐远离初始 x0,直至完全变为噪声。这就是从清晰数据到噪声的前向扩散过程。相对应地也有一个反向过程,即 从噪声中学习如何逐步去除噪声并重建原始数据,这是 diffusion 模型的关键。
对于公式 2 中,q(xt|xt−1) 的均值部分是:√(1−βt)⋅xt−1 其中:
- xt−1 是前一时间步的数据
- βt 是该时间步的预定义扩散程度参数,取值在 (0,1) 之间 将 xt−1 乘以 √(1−βt) 的目的是在每个时间步对前一步的数据进行重新缩放(rescale)。使其逐渐远离初始的 xt=0。这里使用 1−βt 的原因是:
- 当 βt=0 时,√(1−βt)=1,即没有重新缩放
- 当 βt 逼近 1 时,√(1−βt) 逼近 0,即数据被极大程度重新缩放。比如 RGB 通道的 R 通道最大程度的跟原始的像素值改变。
- 所以 √(1−βt) 可以看作是一个重新缩放系数,控制了当前步离初始数据的远近程度。通过设置不同的 βt 值,可以平滑地实现从清晰数据到噪声的转变。
那么,给定原始图像 x0, 能不能一步计算得到加噪任意 t 次后的 xt。这是可以的。
2. 如何一步计算得到加噪 t 步后的结果
假定 αt=1–βt(从增加多少噪声变成保留多少原始图片的信息)和 ˉαt=∏i=1tαi, 那么公式 2 可以改写为:
\begin{aligned}\mathbf{x}_t&= \sqrt{\alpha_t}\mathbf{x}{t-1} + \sqrt{1 – \alpha_t}\boldsymbol{\epsilon}{t-1} & \text{where} \boldsymbol{\epsilon}{t-1}, \boldsymbol{\epsilon}{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\&= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}{t-2} + \sqrt{1 – \alpha_t \alpha{t-1}} \bar{\boldsymbol{\epsilon}}{t-2} & \text{where} \bar{\boldsymbol{\epsilon}}{t-2} \text{merges two Gaussians (*).} \\&= \dots \&= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 – \bar{\alpha}_t}\boldsymbol{\epsilon} \\q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 – \bar{\alpha}_t)\mathbf{I})\end{aligned} \tag{a1}
公式解释,高斯扩散过程中,
- 在时间步 t 的数据 x_t 是如何由上一时间步 t-1 的数据 x_{t-1} 和一个新的高斯噪声 \varepsilon_{t-1} 生成的,可以通过以下公式来描述: x_t = \sqrt{\alpha_t} \cdot x_{t-1} + \sqrt{1 – \alpha_t} \cdot \varepsilon_{t-1} 其中:
- \alpha_t 是变换后的扩散程度参数。
- \varepsilon_{t-1} 是均值为 0,方差为 1 的高斯噪声。
- 通过递推,我们可以将 x_t 表示为初始数据 x_0 和一系列噪声的线性组合: x_t = \sqrt{\alpha_t \cdot \alpha_{t-1}} \cdot x_{t-2} + \text{噪声项}
- 一直递推下去,我们可以得到最终的形式:x_t = \sqrt{\bar{\alpha}_t} \cdot x_0 + \sqrt{1 – \bar{\alpha}_t} \cdot \varepsilon 其中:
- \bar{\alpha}_t 是根据 \alpha_t, \ldots, \alpha_1 计算出的一个量。
- \varepsilon 是将所有先前噪声合并后的一个总噪声项。
最后描述这个过程在时间步 t 的概率分布: q(x_t | x_0) = \mathcal{N}(\sqrt{\bar{\alpha}_t } \cdot x_0, (1 – \bar{\alpha}_t ) \cdot I)
- 其中 \mathcal{N}(\cdot , \cdot) 代表正态分布,其均值为 \sqrt{\bar{\alpha}_t } \cdot x_0,方差为 (1 – \bar{\alpha}_t ) \cdot I。
- 这个过程实际上是从一个已知的初始值 x_0 出发,通过逐步添加噪声到达时间步 t 的一个概率分布描述。它是对之前那个添加单个噪声的过程的延伸和推广。通过这种形式,我们可以明确表示出在任意时间步 t,数据 x_t 同初始 x_0 之间的确定性和随机性的耦合关系。这也为后续的逆扩散过程(去噪过程)提供了理论基础。
3. 前向过程代码
| import torch.nn.functional as F | |
| def linear_beta_schedule(timesteps, start=0.0001, end=0.02): | |
| return torch.linspace(start, end, timesteps) | |
| def get_index_from_list(vals, t, x_shape): | |
| """ | |
| Returns a specific index t of a passed list of values vals | |
| while considering the batch dimension. | |
| """ | |
| batch_size = t.shape[0] | |
| out = vals.gather(-1, t.cpu()) | |
| return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device) | |
| def forward_diffusion_sample(x_0, t, device=device): | |
| """ | |
| Takes an image and a timestep as input and | |
| returns the noisy version of it | |
| """ | |
| noise = torch.randn_like(x_0) | |
| sqrt_alphas_cumprod_t = get_index_from_list(sqrt_alphas_cumprod, t, x_0.shape) | |
| sqrt_one_minus_alphas_cumprod_t = get_index_from_list(sqrt_one_minus_alphas_cumprod, t, x_0.shape) | |
| # mean + variance | |
| return sqrt_alphas_cumprod_t.to(device) * x_0.to(device) \ | |
| + sqrt_one_minus_alphas_cumprod_t.to(device) * noise.to(device), noise.to(device) | |
| # Define beta schedule | |
| T = 300 | |
| betas = linear_beta_schedule(timesteps=T) | |
| # Pre-calculate different terms for closed form | |
| alphas = 1. - betas | |
| alphas_cumprod = torch.cumprod(alphas, axis=0) | |
| #\bar{\alpha}_t = \prod_{i=1}^t \alpha_i, 第一列不变所以用 1 填充 | |
| alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0) | |
| sqrt_recip_alphas = torch.sqrt(1.0 / alphas) | |
| sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod) | |
| sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod) | |
| posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod) |
- 定义了扩散过程的总时间步数 T =300。
betas是一个长度为 T 的序列,表示每个时间步的扩散程度参数 \beta_t。通常使用线性或余弦等策略来设置这个 schedule,这里采用线性 alphas_cumprod = torch.cumprod(alphas, axis=0): 根据 \beta_t 计算出对应的 \alpha_t = 1 – \beta_t。然后计算alphas_cumprod,它表示 \bar{\alpha}t = \prod{i=1}^t \alpha_i,也就是 \alpha_t 值的累积积。alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0): 是计算 \bar{\alpha}_t,也就是在 \bar{\alpha}_t 中去掉最后一项 \alpha_t 的积。由于第一项是 1,所以用F.pad在开头填充 1。sqrt_recip_alphas = torch.sqrt(1.0 / alphas) sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod) sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)分别计算 \sqrt{1/\alpha_t} \ ,\quad \sqrt{\bar{\alpha}_t} \ ,\quad \sqrt{1-\bar{\alpha}_t},后续使用.posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod), 在时间步 t 有 q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 – \bar{\alpha}_t)\mathbf{I}).
| 那么拿一张图片来试试加噪后的效果吧! |
| image = next(iter(dataloader))[0] | |
| plt.figure(figsize=(15,15)) | |
| plt.axis('off') | |
| num_images = 10 | |
| stepsize = int(T/num_images) | |
| for idx in range(0, T, stepsize): | |
| t = torch.Tensor([idx]).type(torch.int64) | |
| # print(idx, t) | |
| plt.subplot(1, num_images+1, int(idx/stepsize) + 1) | |
| img, noise = forward_diffusion_sample(image, t) | |
| show_tensor_image(img) |
这里设置加噪 T = 300 步,显示 10 张图片的话那就是,每隔 30 步打印一次加噪图片:

Inference
[1] Diffusion models from scratch in PyTorch
[2] Diffusion models notebooks
[4] 简单基础入门理解 Denoising Diffusion Probabilistic Model,DDPM 扩散模型

