LLama3 model代码解析

源码来源于:meta-llama/llama3

1.RMSNorm

RMSNorm（Root Mean Square Layer Normalization）与传统的 Layer Normalization 不同，它不计算均值和方差，而是基于均方根（RMS）的归一化。具体来说：

1. 均方根（RMS）计算：

  • 对于一个输入张量 (x)，它的均方根是：
    $$
    \text{RMS}(x) = \sqrt{\frac{1}{d} \sum_{i=1}^d x_i^2}
    $$
    这里，d 是张量的最后一个维度的大小。

2. 归一化：

  • 归一化输入张量 (x)：
    $$
    \hat{x} = \frac{x}{\text{RMS}(x) + \epsilon}
    $$
    这里 $\epsilon$ 是一个小的常数，用于数值稳定性。

3.缩放：

  • 最后，将归一化后的张量乘以一个可训练的参数 (w)：
    $$
    \text{RMSNorm}(x) = \hat{x} \odot w
    $$
    这里 $\odot $ 表示逐元素乘法。

在实现中，我们使用 torch.rsqrt 来计算均方根的倒数，因为这在计算上更高效。公式中的 torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps) 实际上是计算了
$$
\frac{1}{\text{RMS}(x) + \epsilon}
$$

import torch
import torch.nn as nn

class RMSNorm(torch.nn.Module):
    def __init__(self, dim: int, eps: float = 1e-6):
        super().__init__()
        self.eps = eps
        self.weight = nn.Parameter(torch.ones(dim)) #实际训练之后不是全为 1 了

    def _norm(self, x):
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)

    def forward(self, x):
        output = self._norm(x.float()).type_as(x)
        return output * self.weight

# 创建一个 RMSNorm 实例
dim = 4  # 维度大小
rmsnorm = RMSNorm(dim)


x = torch.tensor([[1.0, 2.0, 3.0, 4.0], [2.0, 3.0, 4.0, 5.0]])

print("Input Tensor:")
print(x)
output = rmsnorm(x)
print("Output Tensor after RMSNorm:")
print(output)

2. Rope

1. 引入

详细推导可以查看 旋转式位置编码 (RoPE) 知识总结 、 一文看懂 LLaMA 中的旋转式位置编码（Rotary Position Embedding）和 Inference 1.

对于 query 向量 $ \boldsymbol{q}_m$ 和向量 $ \boldsymbol{k}_n$ 之间的内积，可以用一个函数表示，并且要加入相对位置的变量信息，那么假设为：

$$
\left\langle\boldsymbol{f}{q}\left(\boldsymbol{x}{m}, m\right), f_{k}\left(\boldsymbol{x}{n}, n\right)\right\rangle=g\left(\boldsymbol{x}{m}, \boldsymbol{x}_{n}, m-n\right)\tag{1}
$$

对于函数 f:
$$
f_{q}\left(\boldsymbol{x}{m}, m\right)=\left(\boldsymbol{W}{q} \boldsymbol{x}_{m}\right) e^{i m \theta}\\
f_{k}\left(\boldsymbol{x}{n}, n\right)=\left(\boldsymbol{W}{k} \boldsymbol{x}_{n}\right) e^{i n \theta}\tag{2}
$$

这里，$ \boldsymbol{x}_m $ 和 $ \boldsymbol{x}_n$ 是输入特征向量，分别位于序列中的第 $m$ 和第 $n$ 个位置。$ \boldsymbol{W}_q $ 和 $\boldsymbol{W}_k $ 是线性变换矩阵，用于将输入特征转换为查询（query）和键（key）特征。$\theta$ 是一个与位置相关的固定相位角度。即对应 $m$ 位置的 embedding，加上权重 $ \boldsymbol{W}_q$ 后再引入复数域中的相位因子 $e^{i m \theta}$, 就是 $f$ 表达式了。

那么函数 g, 表示查询和键特征的内积，并且通过取实部来计算实际的相似度或相关性。通过相位差 $e^{i(m-n) \theta} $ 的引入，这个内积捕捉了位置差异带来的相位旋转效应，就实现了对应的即表示内积又引入相对位置关系。
$$
g\left(\boldsymbol{x}{m}, \boldsymbol{x}{n}, m-n\right)=\operatorname{Re}\left[\left(\boldsymbol{W}{q} \boldsymbol{x}{m}\right)\left(\boldsymbol{W}{k} \boldsymbol{x}{n}\right)^{*} e^{i(m-n) \theta}\right] \tag{3}
$$

2. 二维情况

我们从二维情况开始, 这是理解 RoPE 核心思想的基础。

对于二维向量 $\boldsymbol{x}$, 绕原点旋转 $m$ 弧度后, 变成 $\mathbf{R}m \cdot \boldsymbol{x}$。其中, 旋转矩阵 $\mathbf{R}_m$ 的形式如下:

LLama3 model 代码解析

利用三角形和差公式可以得到 $\mathbf{R}_m ^T\mathbf{R}_n=\mathbf{R}{n-m} $, 其中 $n-m$ 就是旋转的相对位置信息。

进一步利用矩阵转置性质, 对于二维向量 $\mathbf{x}$ 和 $\mathbf{y}$, 我们有:

LLama3 model 代码解析

对于注意力机制而言：
$$
\mathbf{a}^{\top} = \text{softmax} \left(\frac{\mathbf{q}^{\top} \mathbf{K}^{\top}}{\sqrt{d_k}} \right) \cdot \mathbf{V} \tag{6}
$$
在注意力机制中, 我们通常计算查询向量和键向量的内积。如果 $\boldsymbol{q}_m$ 和 $\boldsymbol{k}_n$ 是二维向量, 表示位置 $m$ 的查询向量和位置 $n$ 的键向量, 那么它们的注意力分数可以表示为:
$$
S(q_m, k_n) = (\boldsymbol{R}_m \cdot \boldsymbol{q}_m )^T(\boldsymbol{R}_n \cdot \boldsymbol{k}_n ) \tag{7}
$$
其中，$\boldsymbol{R}_m$ 是旋转角度，$\boldsymbol{q}_m $ 是 embedding 乘以可学习的权重的查询特征。$\boldsymbol{R}_m$ 和 $\boldsymbol{R}_n$ 实际上是由 $e^{im\theta}$ 和 $ e^{in\theta}$ 的定义旋转操作。

展开有：

LLama3 model 代码解析

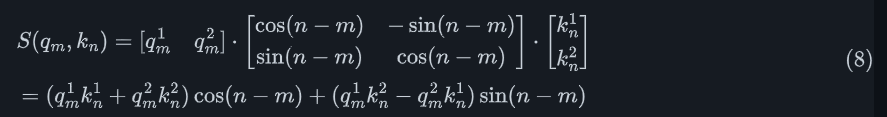
3. 扩展到高维

对于多维情况，RoPE 的核心思想是将向量的维度分组，每两个相邻维度作为一组，然后对每组进行旋转操作。这样可以将二维的旋转概念扩展到高维空间。让我们逐步推导：

  1. 高维旋转矩阵

对于 d 维向量，RoPE 将其分成 d / 2 组，每组 2 个维度。对于第 i 组（i 从 0 开始），旋转角度为 m⋅θi。旋转矩阵 Rm 可以表示为：

LLama3 model 代码解析

其中，每个 $\mathbf{R}_m^{(i)}$ 是一个 2 ×2 的旋转矩阵：

LLama3 model 代码解析
  1. 应用旋转到查询向量

对于查询向量 q，应用旋转后得到 q ’：

$$
\mathbf{q}’_m = \mathbf{R}_m \cdot \mathbf{q}_m
$$

  1. 展开计算

让我们展开这个计算。对于 d 维向量 q，我们可以将其写成：

$$
\mathbf{q}m = [q_0, q_1, q_2, q_3, …, q{d-2}, q_{d-1}]^T
$$

应用旋转后，每一对相邻元素都会发生变化：

$$
\begin{aligned}
q'{2i} &= q{2i} \cos(m\theta_i) – q_{2i+1} \sin(m\theta_i) \\
q'{2i+1} &= q{2i} \sin(m\theta_i) + q_{2i+1} \cos(m\theta_i)
\end{aligned}
$$

  1. 重排项

我们可以将上述表达式重新排列，分离 cos 项和 sin 项：

$$
\begin{aligned}
q'{2i} &= q{2i} \cos(m\theta_i) – q_{2i+1} \sin(m\theta_i) \\
q'{2i+1} &= q{2i+1} \cos(m\theta_i) + q_{2i} \sin(m\theta_i)
\end{aligned}
$$

  1. 矩阵形式

现在，我们可以将这个操作写成矩阵形式：

LLama3 model 代码解析

就是表示每个 q 对应值点乘对应的复数域的旋转值。

4. RoPE 的关键特性

  1. 相对位置编码: 注意力分数只依赖于相对位置 $(n-m)$, 而不是绝对位置。
  2. 平移不变性: 如果我们同时改变 $m$ 和 $n$, 只要它们的差值保持不变, 注意力分数就不会改变。
  3. 线性可组合性: RoPE 保持了线性变换的可组合性, 这使得它可以与现有的预训练模型无缝集成。
  4. 无参数: RoPE 不引入任何额外的可学习参数。
  5. 序列长度外推: 理论上,RoPE 允许模型处理比训练时更长的序列。

5. 实际实现

def precompute_freqs_cis(dim: int, end: int, theta: float =10000.0) -> torch.Tensor:
    """ 为每个位置预计算旋转角度，这些角度在后续的嵌入处理过程中会被用来进行位置编码。通过这种方式，可以在计算注意力权重时隐含地捕捉到输入序列中元素之间的相对位置关系。"""
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[:(dim//2)].float()/dim)) #按照 dim 长度每隔 2 步分配值
    # 生成时间步
    t = torch.arange(end, device=freqs.device, dtype=torch.float32)
    # 计算外积
    freqs = torch.outer(t, freqs)
    # 转换为极坐标表示
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)

    return freqs_cis


def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
    ndim = x.ndim
    assert 0 <= 1 < ndim
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
    return freqs_cis.view(*shape)


def apply_rotary_emb(xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    # 将输入张量转换为复数表示，每两个相邻的实数作为一个复数的实部和虚部
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))

    # 调整 freqs_cis 的形状以便于广播
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)

    # 应用旋转（复数乘法），然后转回实数表示
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)

    return xq_out.type_as(xq), xk_out.type_as(xk)

3. 模型结构

LLama 模型部分参数，实际参考官方源码，非常清晰的结构，易于理解。

@dataclass
class ModelArgs:
    dim: int = 4096
    n_layers: int = 32
    n_headers: int = 32
    n_kv_heads: Optional[int] = None
    vocab_size: int = -1
    multiple_of: int = 256 #表示相关的参数（例如前馈层的维度）应当是 256 的倍数
    ffn_dim_multiplier: Optional[float] = None
    norm_eps: float = 1e-5
    rope_theta: float = 500000

    max_batch_size: int = 32
    max_seq_len: int = 2048

主要改进：

  1. 使用 ROPE (Rotary Position Embedding)：
    Llama 3.1 引入了 ROPE 机制，利用旋转位置嵌入来更好地捕捉位置编码信息。这种方法使用较大的 theta 值（500000），以适应更长文本的处理。这使得模型在处理长文本时能更好地保持序列中元素的相对位置关系，提高文本理解和生成的质量。
  2. 使用 KV Cache 提升计算效率 ：
    通过使用键 - 值缓存（KV Cache），Llama 3.1 显著提升了计算效率。在生成长文本时，模型仅需计算新的查询（query）与缓存中的键（key）和值（value）的关系，而无需重复计算所有先前步骤。这种方法大幅减少了计算量，尤其在处理长序列时，显著提升了模型的响应速度和效率。
  3. 大规模并行技术 ：
    Llama 3.1 大量使用了来自 Fairscale 库的ColumnParallelLinear 和RowParallelLinear等技术。这些技术通过在列和行方向上的并行计算，优化了模型的矩阵乘法操作，降低了计算复杂度。通过将线性层分解为多个并行处理单元，模型能够更高效地利用硬件资源，提升整体性能。
  4. 使用 RMSNorm 减少计算量 ：
    采用 RMSNorm（Root Mean Square Layer Normalization）代替传统的 LayerNorm，进一步减少了计算量。RMSNorm 通过仅计算输入的均方根值（而非均值和方差）来进行归一化处理，减少了计算开销。同时，这种方法在保持模型性能的前提下，简化了归一化过程，使得模型更高效。

另外 LLama 3.1 优化的地方还有：增加的上下文长度和 GQA，跨文档注意力 ， 多语言支持 (增加多语言数据)， 工具调用和扩展性 ， 安全性和指令优化 。下面是Transformer 代码：

class Transformer(nn.Module):
    def __init__(self, params: ModelArgs):
        super().__init__()
        self.params = params
        self.vocab_size = params.vocab_size
        self.n_layers = params.n_layers


        self.tok_embedding = VocabParallelEmbedding(
            params.vocab_size,
            params.dim,
            init_method=lambda x: x
        )
        self.layers = torch.nn.ModuleList()
        #设值多层 TransformerBlock
        for layer_id in range(params.n_layers):
            self.layers.append(TransformerBlock(layer_id, params))

        self.norm = RMSNorm(params.dim, eps=params.norm_eps)
        self.output = ColumnParallelLinear(
            params.dim,
            params.vocab_size,
            bias=False,
            init_method=lambda x: x
        )

        self.freqs_cis = precompute_freqs_cis(params.dim//params.n_headers,
                                              params.max_seq_len*2,
                                              params.rope_theta
                                              )

    def forward(self, tokens: torch.Tensor, start_pos: int):
        _bsz, seq_len = tokens.shape
        h = self.tok_embedding(tokens)
        self.freqs_cis = self.freqs_cis.to(h.device)
        freqs_cis = self.freqs_cis[start_pos: start_pos + seq_len]

        mask = None
        if seq_len > 1:
            mask = torch.full((seq_len, seq_len), float("-inf"), device=tokens.device)
            mask = torch.triu(mask, diagonal=1) #上三角矩阵

            #已经生成的 cache 不用参与计算和 mask 拼在一起, 构成新的 mask
            mask = torch.hstack([torch.zeros((seq_len, start_pos), device=tokens.device), mask]
            ).type_as(h)

        #多层 transformer
        for layer in self.layers:
            h = layer(h, start_pos, freqs_cis, mask)
        h = self.norm(h)

        output = self.output(h).float()

        return output

Inference

[1] Transformer 升级之路：2、博采众长的旋转式位置编码

[2] llama 3.1 新技术

正文完
LLaMA LLama3.1 LLM
发表至： llm NLP
2024-07-31
 
admin
版权声明：本站原创文章，由 admin 2024-07-31发表，共计7342字。
转载说明：除特殊说明外本站文章皆由CC-4.0协议发布，转载请联系tensortimes@gmail.com。
LLaMA-Factory 训练
开源Qwen2-VL模型发布：多模态大模型家族的新成员
基于gemini SQL问答
LLM模型参数
评论（没有评论）
验证码